Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha!
c) Các tam giácACM và BDM cân tại C và D; CO là phân giác góc ACM; DO là phân giác góc BDM => Các đường phân giác này cũng là đường cao => CO vuông góc với AM tại E và DO vuông góc với BM tại F => g. OEM = OFM = 90o.
Mặt khác g.AMB =90o(Góc nội tiếp chắn nửa đường tròn) => Từ giác OEMF là hình chữ nhật => I là trung điểm của OM => IO = OM/2 = R/2 (Không đổi)
Do đó khi M di chuyển thì trung điểm I của EF luôn cách O một khoảng không đổi R/2 => Quỹ tích trung điểm I của EF là nửa đường tròn tâm O bán kính R/2 cùng phía với nửa đường trón tâm O đường kính AB.

Bạn tự vẽ hình nha!
c) Các tam giác ACM và BDM cân tại C và D; CO là phân giác góc ACM; DO là phân giác góc BDM => Các đường phân giác này cũng là đường cao => CO vuông góc với AM tại E và DO vuông góc với BM tại F => g. OEM = OFM = 90o.
Mặt khác g.AMB =90o(Góc nội tiếp chắn nửa đường tròn) => Từ giác OEMF là hình chữ nhật => I là trung điểm của OM => IO = OM/2 = R/2 (Không đổi)
Do đó khi M di chuyển thì trung điểm I của EF luôn cách O một khoảng không đổi R/2 => Quỹ tích trung điểm I của EF là nửa đường tròn tâm O bán kính R/2 cùng phía với nửa đường trón tâm O đường kính AB.

a) Ta có: CD là tiếp tuyến của (O) tại M (gt)
=> CM \(\perp\)MO => \(\widehat{CMO}=90^o\)
AC là tiếp tuyến của (O) tại A (gt)
=> \(AC\perp AO\Rightarrow\widehat{CAO}=90^o\)
Xét tứ giác OACM có: \(\widehat{CMO}+\widehat{CAO}=90^o+90^o=180^o\)
=> OACM nội tiếp (1)
Chứng minh Tương tự : OBDM nội tiếp (2)
b) M thuộc (O), AB là đường kính
=> \(\widehat{EMF}=\widehat{AMB}=90^o\)( góc chắn nửa đường tròn) (3)
Ta có: \(CO\perp AM\)( tự chứng minh bài toán quen thuộc )
=> \(\widehat{OEM}=90^o\)(4)
Tương tự \(\widehat{OFM}=90^o\)(5)
Từ 3, 4, 5 => Tứ giác OEFM là hình chữ nhật (tứ giác có 3 góc vuông ) (6)
c) Ta có: \(\widehat{IOK}=\widehat{EOF}=90^o\)( theo 6)
Mặt khác: I là trung điểm OC, tam giác CMO vuông tại M
=> CM=IC=IO=> tam giác CIM cân => \(\widehat{IMC}=\widehat{MCI}\)
mà \(\widehat{MCI}=\widehat{MCO}=\widehat{MAO}\)( từ 1)
=> \(\widehat{IMC}=\widehat{MAO}\), chứng minh tương tự \(\widehat{KMD}=\widehat{MBO}\)
=> \(\widehat{IMC}+\widehat{KMD}=\widehat{MAO}+\widehat{MBO}=90^o\)Vì tam giác AMB vuông tại M
=> \(\widehat{IMK}=90^o\)
Xét tứ giác OIMK có: \(\widehat{IMK}+\widehat{IOK}=180^o\)
=> OIMK nội tiếp
d) IK là đường trung bình của tam giác COD =>IK=1/2CD và OH=1/2 OM (Với H là giao điểm OM và IK=> OH vuông IF)
=> \(S_{\Delta IOK}=\frac{1}{4}S_{\Delta OCD}\)
Tam giác IKM= tam giác IKO (c.c.c)
=> \(S_{\Delta IOK}=S_{\Delta IMK}\)
=> \(S_{IMKO}=S_{\Delta IOK}+S_{\Delta IMK}=\frac{1}{2}S_{\Delta COD}\)
Ta lại có: tam giác COM= tam giác COA , tam giác MOD=tam giác BOD
=> \(S_{COD}=S_{\Delta COM}+S_{\Delta MOD}=\frac{1}{2}S_{CAMO}+\frac{1}{2}S_{MDBO}=\frac{1}{2}S_{ACDB}\)
=> \(S_{IMKO}=\frac{1}{4}S_{ACDB}=\frac{1}{4}.\frac{1}{2}\left(AC+DB\right).AB\)=10 (cm)vì ACDB là hình thang vuông với đáy AC, DB và đường cao AB

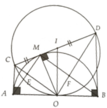
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

Bạn tự vẽ hình nhé :
1.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\)
\(\Rightarrow CAOM\)nội tiếp đường tròn đường kính OC
Tương tự DMOB nội tiếp đường tròn đường kính OD
2 . Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM=CA,OC\) là phân giác \(\widehat{AOM}\)
Tương tự DM = DB , OD là phân giác ^BOM
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\)
\(\Rightarrow OC\perp OD\)
Lại có ; \(OM\perp CD\Rightarrow CM.DM=OM^2\Rightarrow CM.DM=R^2\)
Mà : \(CM=CA,DM=DB\Rightarrow AC.BD=R^2\Rightarrow AC.3R=R^2\Rightarrow AC=\frac{R}{3}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}AB\left(BD+CA\right)=\frac{1}{2}.2R.\left(3R+\frac{R}{3}\right)=\frac{10R^2}{3}\)
3.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CO\perp AM=E\) là trung điểm AM
Tương tự \(OD\perp BM=F\) là trung điểm BM
\(\Rightarrow MN\) là đường trung bình \(\Delta ABC\Rightarrow EF//MN\)
Mà \(OE\perp ME,OF\perp MF,MN\perp ON\)
\(\Rightarrow M,E,N,O,F\in\) đường tròn đường kính OM
\(\Rightarrow EFNO\) nội tiếp
\(\Rightarrow\widehat{EFO}+\widehat{ENO}=180^0\)
Mà \(\widehat{NEF}+\widehat{ENO}=180^0\) ( EF // AB => EF//NO )
\(\Rightarrow EFON\) là hình thang cân