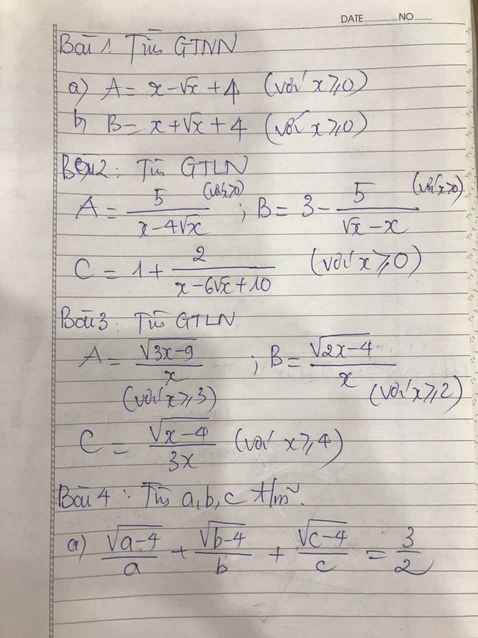mình dở toán hình lắm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 7 2021
B1)
b, Có \(x\ge0\Rightarrow B=x+\sqrt{x}+4\ge0+0+4=4\)
Dấu "=" xảy ra khi x=0
Vậy \(B_{min}=4\)
3 tháng 7 2021
Bài 1 :
\(b,B=x+\sqrt{x}+4=x+2.\sqrt{x}.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{15}{4}\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\)
Thấy : \(\sqrt{x}+\dfrac{1}{2}\ge\dfrac{1}{2}\)
\(\Rightarrow B=\left(\sqrt{x}+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ge4\)
Vậy \(Min_B=4\Leftrightarrow x=0\)
26 tháng 9 2021
\(=\sqrt{3}-1+\sqrt{\left(6-\sqrt{3}\right)^2}=\sqrt{3}-1+6-\sqrt{3}=5\)
26 tháng 9 2021
\(\sqrt{\left(\sqrt{3}-1\right)^2}+\sqrt{39-2\sqrt{108}}\)
\(=\sqrt{3}-1+6-\sqrt{3}\)
=5
24 tháng 2 2022
a, Vì D là trung điểm BC => OD vuông BC
AM là tiếp tuyến với M là tiếp điểm nên ^AMO = 900
Xét tứ giác AMOD ta có
^AMO + ^ADO = 1800
mà 2 góc này đối
Vậy tứ giác AMOD nt 1 đường tròn
b, Xét tam giác AMB và tam giác ACM ta có
^AMB = ^ACM ( cùng chắn cung MB )
^A _ chung
Vậy tam giác AMB ~ tam giác ACM (g.g)
=> AM/AC = AB/AM => AM^2 = AB.AC
c, bạn ktra lại đề
20 tháng 10 2021
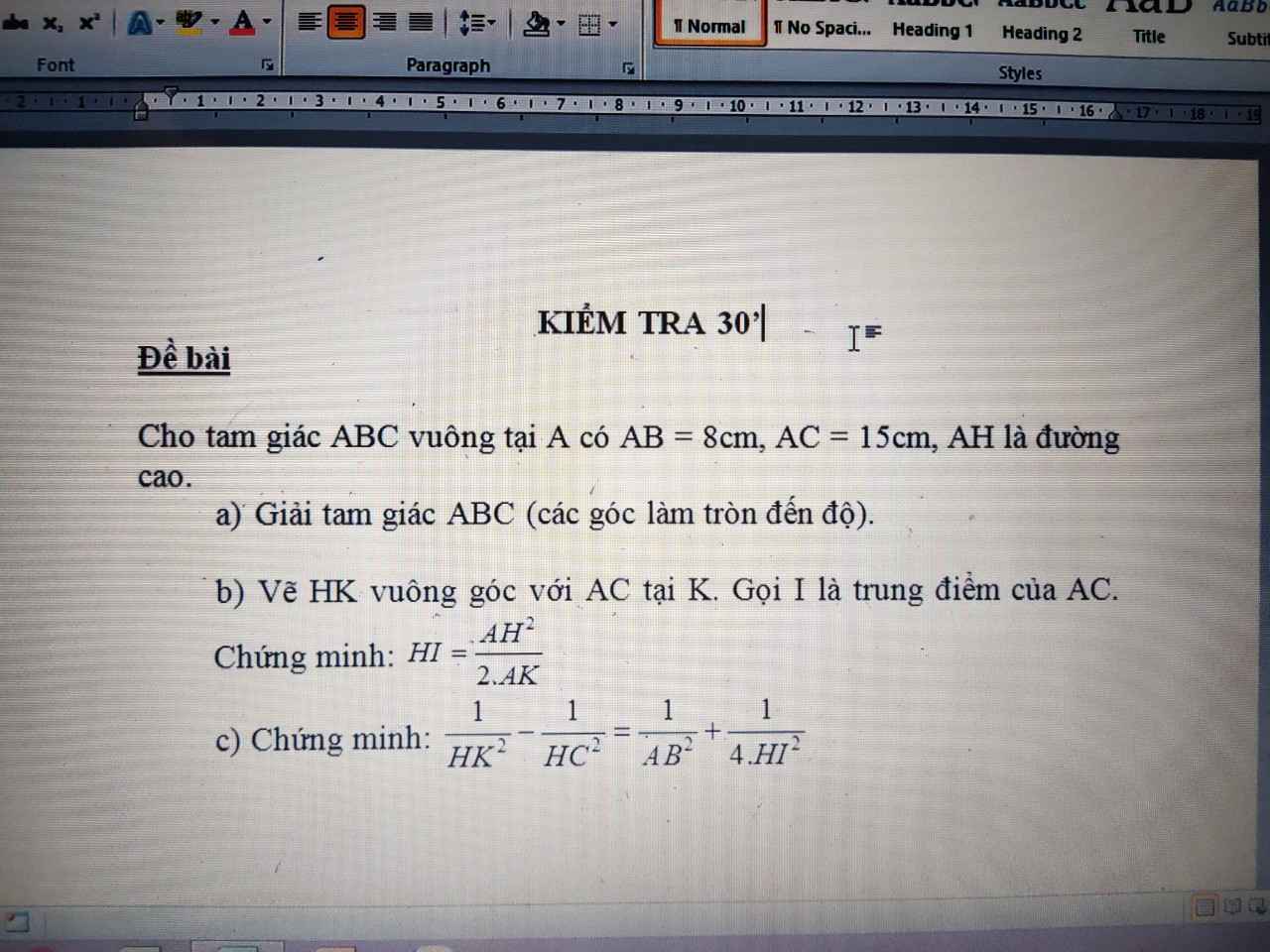
b: Xét ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC
nên \(AH^2=AC\cdot AK\)
\(\Leftrightarrow\dfrac{AC}{2}=\dfrac{AH^2}{2\cdot AK}\)
hay \(HI=\dfrac{AH^2}{2\cdot AK}\)
28 tháng 10 2021
a, Ta có \(\widehat{ACD}=90^0\) (góc nt chắn nửa đg tròn) nên CD⊥AC
Do đó CD//BE
Ta có \(\widehat{ABD}=90^0\) (góc nt chắn nửa đg tròn) nên BD⊥AB
Do đó BD//CF
Vậy BHCD là hbh
24 tháng 2 2022
bạn đăng tách ra nhé
1, Lấy vế cộng vế ta được \(\dfrac{4}{x-2}=4\Rightarrow x-2=1\Leftrightarrow x=3\)
Thay vào ta được \(\dfrac{2}{3-2}-\dfrac{3}{y+1}=1\Rightarrow\dfrac{3}{y+1}=1\Rightarrow y+1=3\Leftrightarrow y=2\)
