K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 9 2021
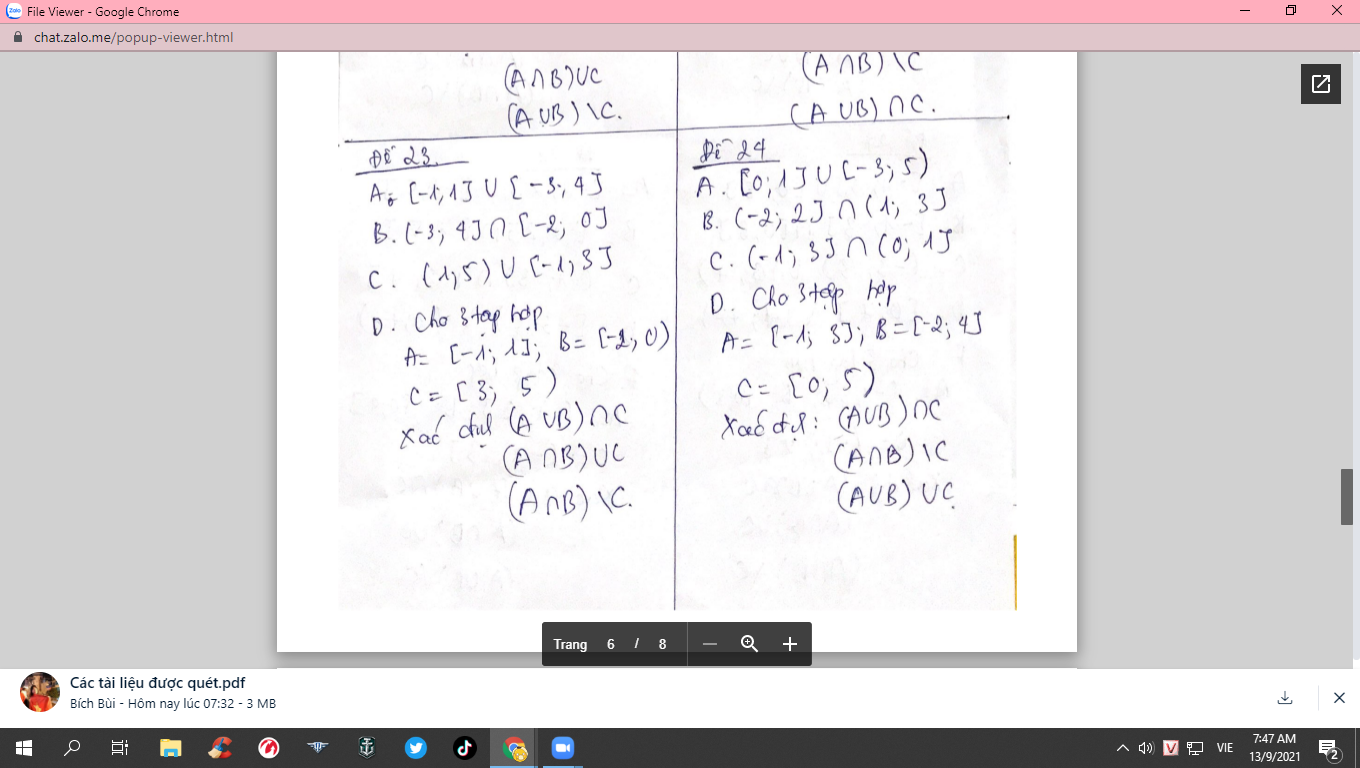
\(a,A=\left\{-3;-2;-1;0;1;2;3;4\right\}\\ b,B=\left\{2\right\}\\ c,C=\left\{1\right\}\\ d,\left(A\cup B\right)\cap C=\left\{0;1;2;3;4\right\}\\ \left(A\cap B\right)\ C=\left\{-1\right\}\\ \left(A\cup B\right)\cup C=\left\{-2;-1;0;1;2;3;4\right\}\)
13 tháng 9 2021
câu \(d,\) ý 2 mình ghi nhầm nha bạn, sửa lại:
\(\left(A\cap B\right)\C=\left\{-1\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 12 2021
Phương trình đã cho có 2 nghiệm phân biệt khi:
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=m^2-m\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m\ne2\end{matrix}\right.\)
b.
Theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m}{m-2}\\x_1x_2=\dfrac{m}{m-2}\end{matrix}\right.\)
\(Q=\dfrac{1}{x_1}+\dfrac{1}{x_2}+2017=\dfrac{x_1+x_2}{x_1x_2}+2017\)
\(=\dfrac{-2m}{m-2}.\dfrac{m-2}{m}+2017=-2+2017=2015\) là hằng số (đpcm)
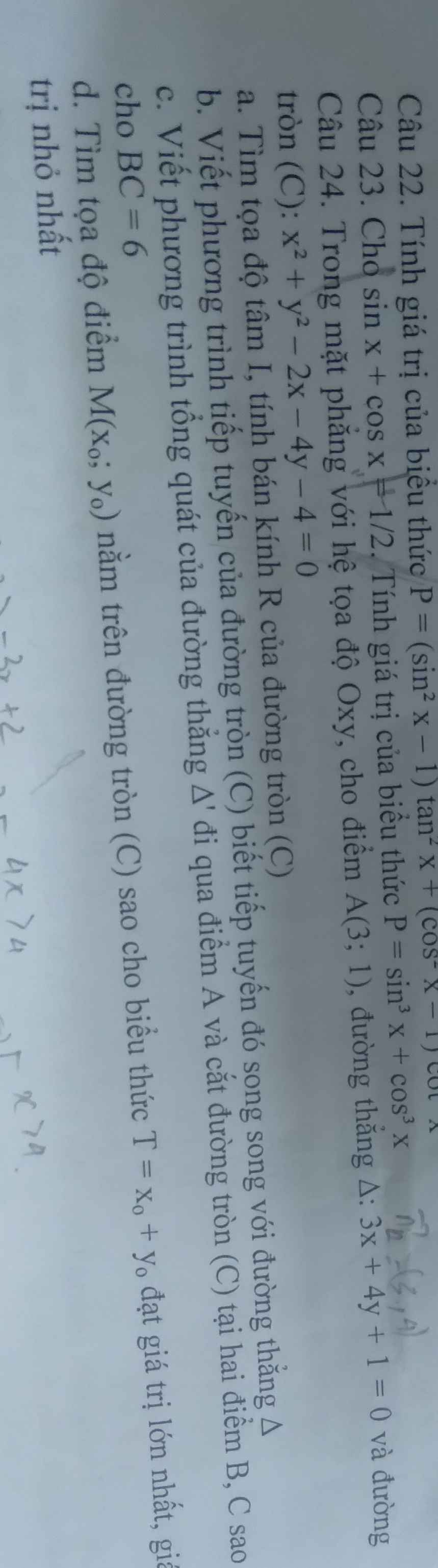
24:
a: x^2+y^2-2x-4y-4=0
=>x^2-2x+1+y^2-4y+4-9=0
=>(x-1)^2+(y-2)^2=9
=>R=3 và I(1;2)
b: Δ: 3x+4y+1=0
Gọi (d) là phương trình cần tìm
(d)//Δ nên (d): 3x+4y+c=0
R=3; I(1;2)
Vì (d) là tiếp tuyến của (C) nên ta có:
d(I;(d))=R=3
=>\(\dfrac{\left|1\cdot3+2\cdot4+c\right|}{\sqrt{3^2+4^2}}=3\)
=>|c+11|=15
=>c=4 hoặc c=-26