K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 7 2021
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC
NA
19 tháng 5 2021
a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được
NT
1
29 tháng 7 2021
Bài 3:
c) Ta có: \(\dfrac{2-x}{5}=\dfrac{x+4}{7}\)
\(\Leftrightarrow14-7x=5x+20\)
\(\Leftrightarrow-7x-5x=20-14\)
\(\Leftrightarrow-12x=6\)
hay \(x=-\dfrac{1}{2}\)
15 tháng 7 2021
Câu 4:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Xét ΔABC có AB<AC<BC(9cm<12cm<15cm)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
b) Xét ΔABC vuông tại A và ΔAEC vuông tại A có
AB=AE(gt)
AC chung
Do đó: ΔABC=ΔAEC(Hai cạnh góc vuông)
15 tháng 7 2021
c) Xét ΔCEB có
CA là đường trung tuyến ứng với cạnh BE(gt)
BH là đường trung tuyến ứng với cạnh CE(gt)
CA cắt BH tại M(gt)
Do đó: M là trọng tâm của ΔCBE(Tính chất ba đường trung tuyến của tam giác)
Suy ra: \(CM=\dfrac{2}{3}CA\)
hay \(CM=\dfrac{2}{3}\cdot12=8\left(cm\right)\)
d) Xét ΔCEB có
A là trung điểm của BE(gt)
AK//CE(gt)
Do đó: K là trung điểm của BC(Định lí 1 đường trung bình của tam giác)
Xét ΔCBE có
M là trọng tâm của ΔCBE(cmt)
EK là đường trung tuyến ứng với cạnh BC(cmt)
Do đó: E,M,K thẳng hàng(đpcm)
4 tháng 2 2022
Bài 19:
a: \(A=5x+\dfrac{1}{9}y=5\cdot\dfrac{-1}{10}+\dfrac{1}{9}\cdot4.8=\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(A=x-\dfrac{2}{3}=\dfrac{-1}{3}-\dfrac{2}{3}=-1\)
4 tháng 2 2022
\(a,7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+\dfrac{1}{9}y\\ =5.\left(\dfrac{-1}{10}\right)+\dfrac{1}{9}.4,8\\ =\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{1}{30}\\ b,x=\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{-7}{40}+\dfrac{5}{11}}{\dfrac{21}{80}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{123}{440}}{\dfrac{-369}{880}}=\dfrac{-1}{3}+\dfrac{-2}{3}=\dfrac{-3}{3}=\left(-1\right)\)
27 tháng 8 2021
6) \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)
7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)
8) \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)
9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
10) \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)
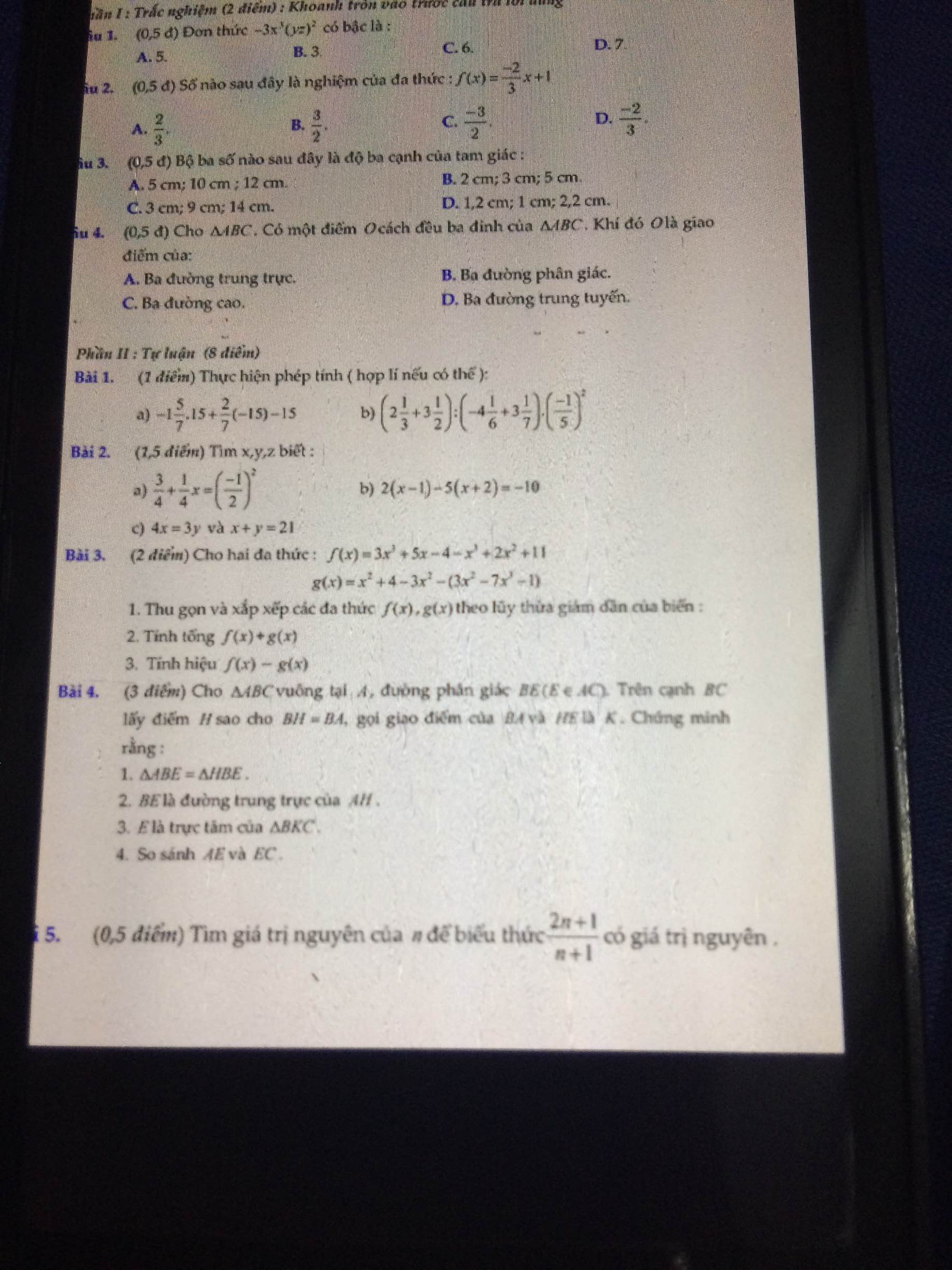
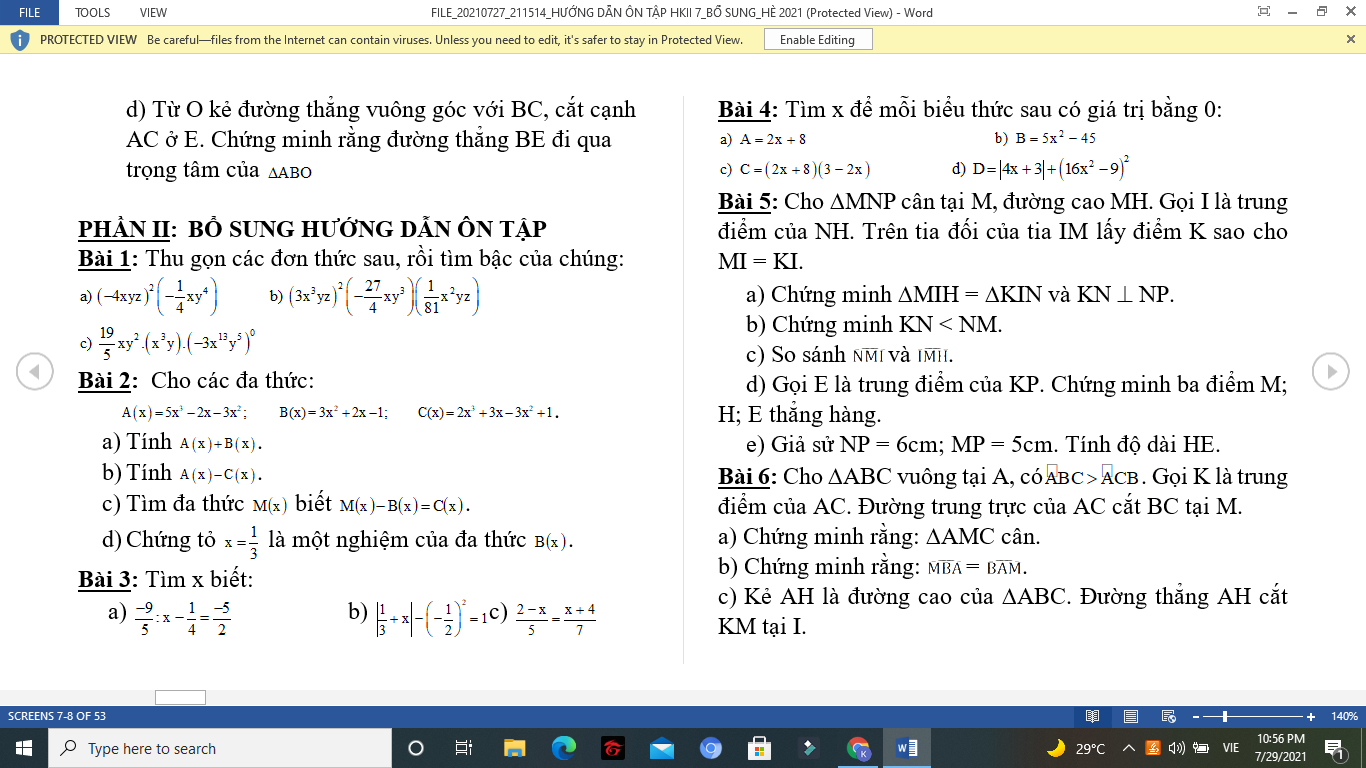
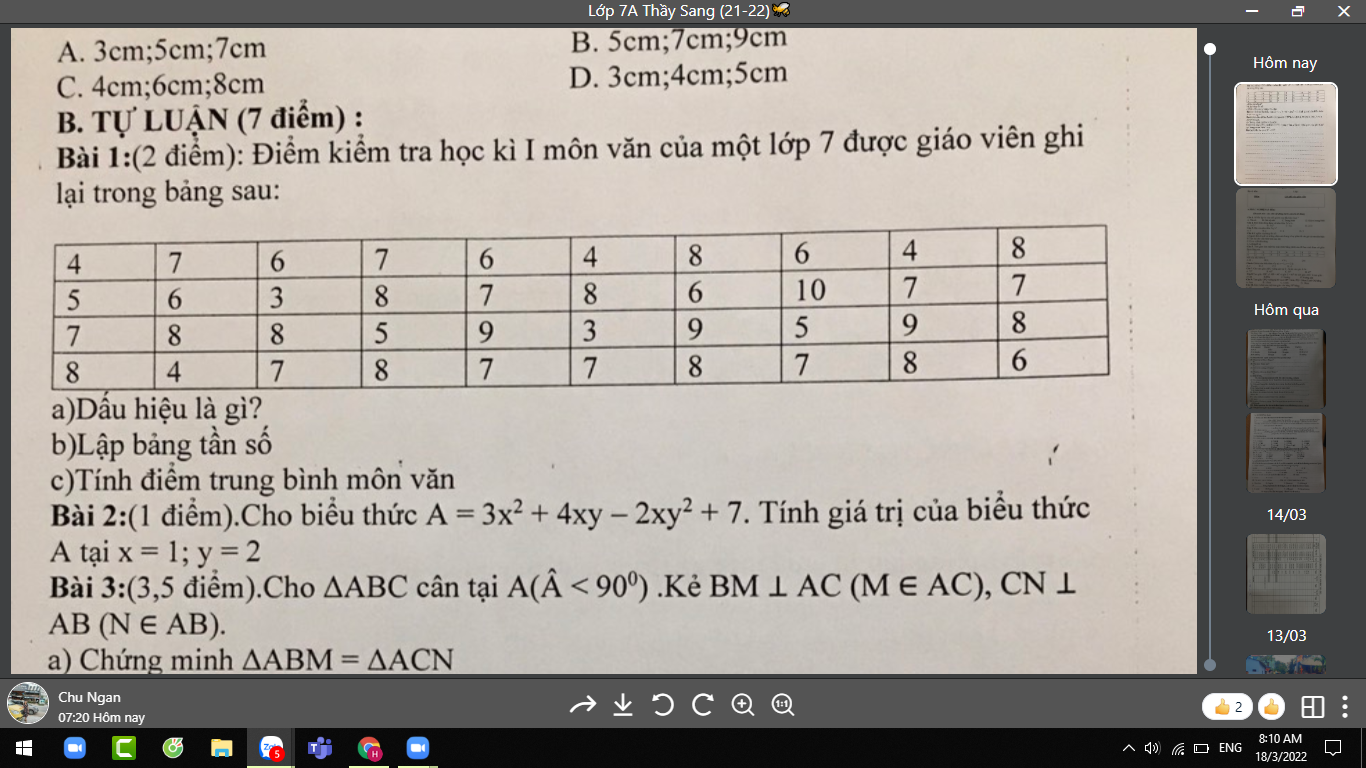giúp mình câu b bài 1 đc ko ạ
Bài 5:
a: \(C=A\cdot B=\dfrac{-1}{3}\cdot\dfrac{3}{2}\cdot x^3y\cdot x^2yz=-\dfrac{1}{2}x^5y^2z\)
b: Hệ số là -1/5
Biến là \(x^5;y^2;z\)
Bậc là 8
c: \(C=\dfrac{1}{2}\cdot\left(-1\right)^5\cdot2^2\cdot3=-\dfrac{1}{2}\cdot4\cdot3=-2\cdot3=-6\)
cảm ơn bạn nhìu!!!