
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
ĐKXĐ: $x>0; x\neq 1$
\(A=\frac{(\sqrt{x}-1)(x+\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}-\frac{(\sqrt{x}+1)(x-\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+1)}+\frac{x+1}{\sqrt{x}}\)
\(=\frac{x+\sqrt{x}+1}{\sqrt{x}}-\frac{x-\sqrt{x}+1}{\sqrt{x}}+\frac{x+1}{\sqrt{x}}=\frac{x+\sqrt{x}+1-(x-\sqrt{x}+1)+(x+1)}{\sqrt{x}}\)
\(=\frac{x+2\sqrt{x}+1}{\sqrt{x}}=\frac{(\sqrt{x}+1)^2}{\sqrt{x}}\)
Bài 2:
\(\frac{x+2}{x\sqrt{x}+1}+\frac{\sqrt{x}-1}{x-\sqrt{x}+1}-\frac{\sqrt{x}-1}{x-1}\)
\(=\frac{x+2}{(\sqrt{x}+1)(x-\sqrt{x}+1)}+\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{\sqrt{x}-1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{x+2+x-1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{1}{\sqrt{x}+1}=\frac{2x+1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{x-\sqrt{x}+1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}\)
\(=\frac{2x+1-(x-\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}=\frac{x+\sqrt{x}}{(\sqrt{x}+1)(x-\sqrt{x}+1)}\)
\(=\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}=\frac{\sqrt{x}}{x-\sqrt{x}+1}\)
Theo BĐT Cô-si:
$x+1\geq 2\sqrt{x}\Rightarrow x-\sqrt{x}+1\geq \sqrt{x}$
$\Rightarrow B\leq \frac{\sqrt{x}}{\sqrt{x}}=1$
Dấu "=" xảy ra khi $x=1$ (không thỏa mãn vì $x\neq 1$)
$\Leftrightarrow B< 1$

\(\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
\(\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\)
\(\widehat{ABC}=90^0\) (góc nội tiếp chắn nửa đường tròn)

bài 2
a) ĐKXĐ: a\(\ge\)0, a\(\ne\)1
b)P=\(\dfrac{1+\sqrt{a}-1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\).\(\dfrac{1+\sqrt{a}}{\sqrt{a}}\)
P=\(\dfrac{2\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}.\dfrac{1+\sqrt{a}}{\sqrt{a}}\)
P=\(\dfrac{2}{1-\sqrt{a}}\)
c) thay a=4 vào biểu thức ta có
P=\(\dfrac{2}{1-\sqrt{4}}\)=\(\dfrac{2}{1-2}\)=-2
d) để P=9 thì
\(\dfrac{2}{1-\sqrt{a}}=9\)\(\Rightarrow\)2=9(1-\(\sqrt{a}\))
\(\Rightarrow\)2=9-\(9\sqrt{a}\)\(\Rightarrow\)\(9\sqrt{a}=7\)\(\Rightarrow\)\(\sqrt{a}=\dfrac{7}{9}\)
\(\Rightarrow a=\dfrac{49}{81}\)
bài 3
a) \(\sqrt{9x^2}=4\Rightarrow3x=4\)\(\Rightarrow\)\(x=\dfrac{4}{3}\)
b)\(\Rightarrow\)\(\left(x-\sqrt{5}\right)^2\)=0\(\Rightarrow x-\sqrt{5}=0\)
\(\Rightarrow x=\sqrt{5}\)

1
Có: \(tgB=\dfrac{CA}{CB}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
\(cotgB=\dfrac{CB}{CA}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)
Vì A, B phụ nhau nên:
\(cotgA=tgB=\dfrac{3}{4}\\ tgA=cotgB=\dfrac{4}{3}\)
Áp dụng pytago vào tam giác ABC vuông tại C, có:
\(AB^2=BC^2+AC^2=1,2^2+0,9^2=1,5^2\Rightarrow AB=1,5\left(vì.AB>0\right)\)
Do đó: \(sinB=\dfrac{CA}{AB}=\dfrac{0,9}{1,5}=\dfrac{3}{5};cosB=\dfrac{CB}{BA}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)
Vì A, B phụ nhau nên:
\(sinA=cosB=\dfrac{4}{5};cosA=sinB=\dfrac{3}{5}\)
3:
a: Xét ΔBAC có AB^2=CA^2+CB^2
nên ΔABC vuông tại C
b: sin A=cos B=BC/AC=căn 15/5
cos A=sin A=CA/BC=căn 2/5=1/5*căn 10
tan A=cot B=căn 15/căn 10=căn 3/2
cot A=tan B=căn 2/3

3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM

Bài 1:
a: \(\Leftrightarrow2x^2+5x-2x-5=0\)
=>(2x+5)(x-1)=0
=>x=-5/2 hoặc x=1
c: \(\Leftrightarrow\left\{{}\begin{matrix}8x+4y=4\\3x+4y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=5\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

a: Xét tứ giác AOMN có
\(\widehat{NAO}+\widehat{NMO}=180^0\)
Do đó: AOMN là tứ giác nội tiếp
Xét (O) có
NM là tiếp tuyến
NA là tiếp tuyến
Do đó: NM=NA
Xét (O) có
PM là tiếp tuyến
PB là tiếp tuyến
Do đó: PM=PB
Ta có: NP=MN+MP
nên NP=AN+BP
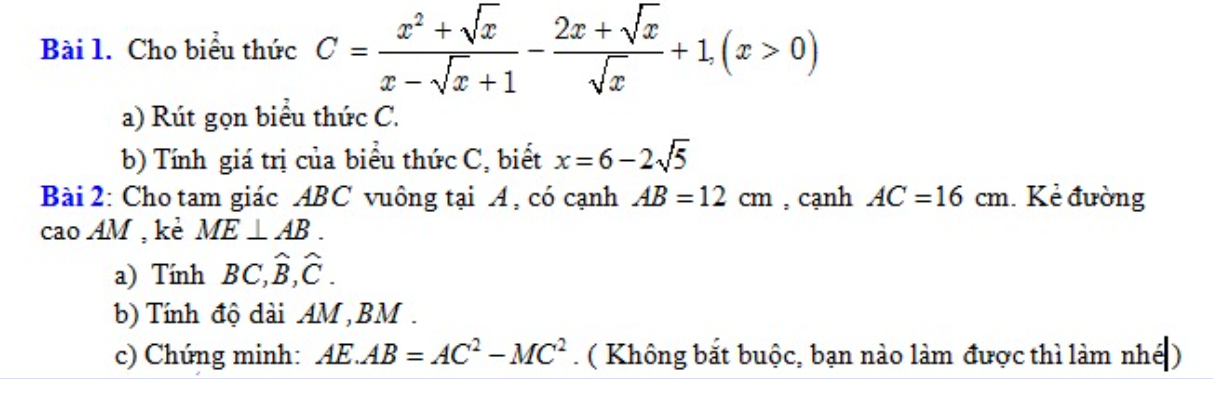
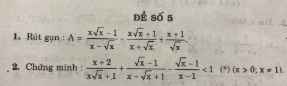 Mn giúp mình bài 2 vs ạ
Mn giúp mình bài 2 vs ạ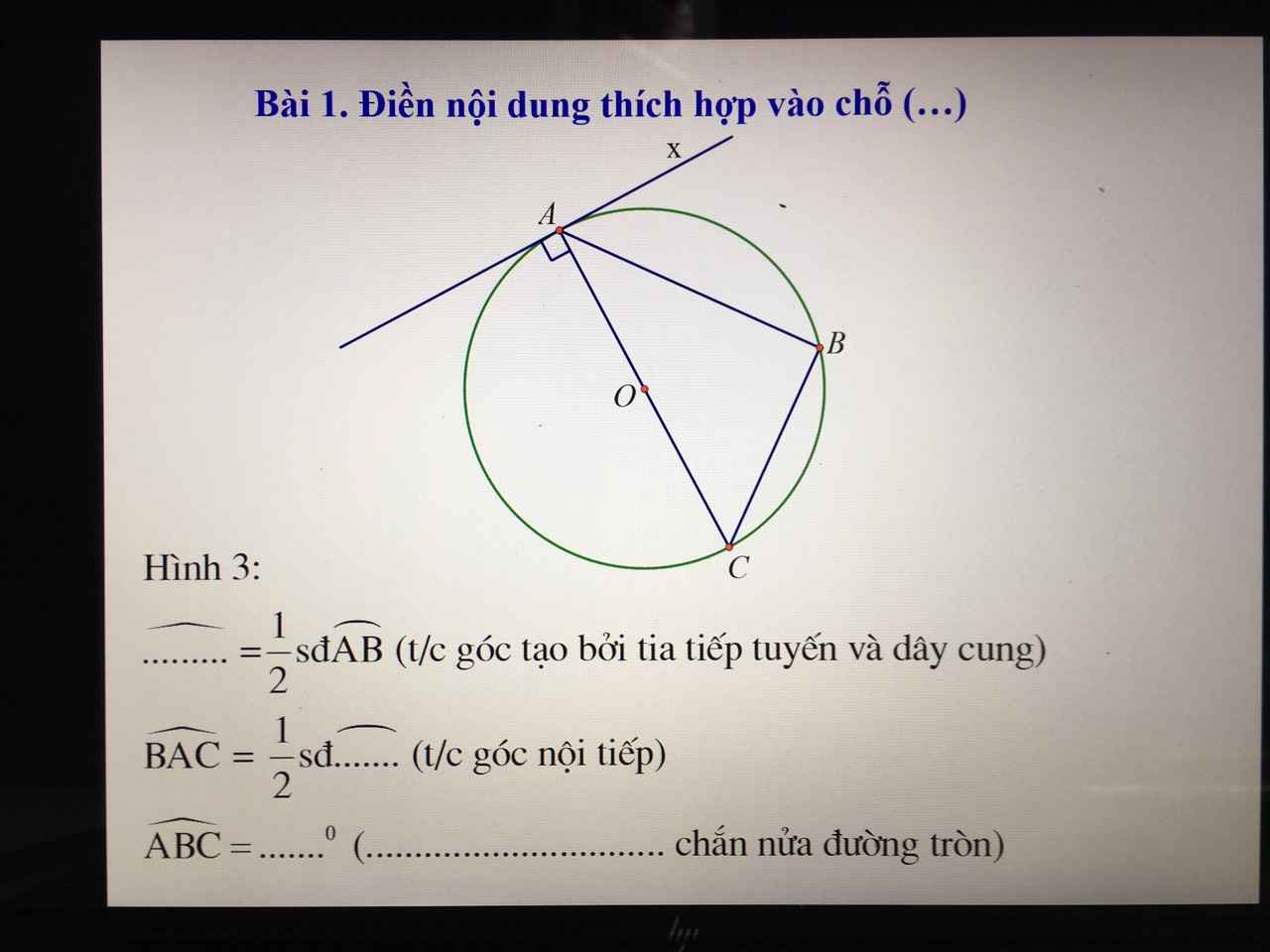







Bài 1:
a: Ta có: \(C=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+1\)
\(=x+\sqrt{x}-2\sqrt{x}-1+1\)
\(=x-\sqrt{x}\)