K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 10 2021
bạn tự vẽ hình giúp mik nha
a.ta có \(\Delta\)ABC nội tiếp (O) và AB là đường kính nên \(\Delta\)ABC vuông tại C
trong \(\Delta ABC\) vuông tại C có
AC=AB.cosBAC=10.cos30=8,7
BC=AB.sinCAB=10.sin30=5
ta có Bx là tiếp tuyến của (O) nên Bx vuông góc với AB tại B
trong \(\Delta\)ABE vuông tại B có
\(cosBAE=\dfrac{AB}{AE}\Rightarrow AE=\dfrac{AB}{cosBAE}=\dfrac{10}{cos30}=11,5\)
mà:CE=AE-AC=11,5-8,7=2,8
b.áp dụng pytago vào \(\Delta ABE\) vuông tại B có
\(BE=\sqrt{AE^2-AB^2}=\sqrt{11,5^2-10^2}=5,7\)
DH
1
23 tháng 9 2021
Xét tam giác ABH vuông tại H có:
\(sinB=\dfrac{AH}{AB}=0,5\Rightarrow AB=\dfrac{AH}{0,5}=\dfrac{5}{0,5}=10\)
Xét tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\left(Pytago\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-5^2}=5\sqrt{3}\)
DH
0
3 tháng 9 2021
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
24 tháng 1 2023
a: Xét (O) có
EM,EA là tiếp tuyến
nên EM=EA và OE là phân giác của góc MOA(1)
Xét (O) có
FM,FB là tiếp tuyến
nên FM=FB và OF là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc FOE=1/2*180=90 độ
b: EF=EM+MF
=>EF=EA+FB
c: Xét ΔOEF vuông tại O có OM là đường cao
=>ME*MF=OM^2
=>ME*MF=OA^2
3 tháng 7 2023
5:
a: góc ACB=1/2*180=90 độ
Xét ΔAKH vuông tại K và ΔACB vuông tại A có
góc KAH chung
=>ΔAKH đồng dạng với ΔACB
b: Xét ΔADC và ΔBEC có
AD=BE
góc DAC=góc EBC
AC=BC
=>ΔADC=ΔBEC
=>DC=EC
=>ΔDEC cân tại C
góc CAB=45 độ
=>góc CDE=góc CAB=45 độ
=>ΔCDE vuông cân tại C
ML
0
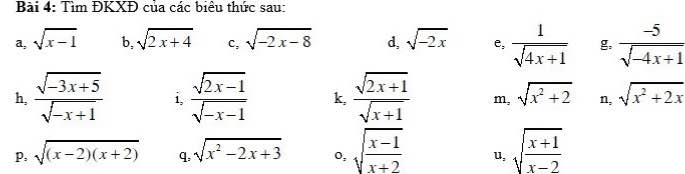
a: ĐKXĐ: \(x\ge1\)
b: ĐKXĐ: \(x\ge-2\)
c: ĐKXĐ: \(x\le-2\)
d: ĐKXĐ: \(x\le0\)
đúng