
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ACMD co
góc ACD=góc AMD=90 độ
=>ACMD là tứ giác nội tiếp
b: Xet ΔCHA vuông tại C và ΔCBD vuông tại C co
góc CAH=góc CDB
=>ΔCHA đồng dạng với ΔCBD
=>CH/CB=CA/CD
=>CH*CD=CA*CB
c: Xét ΔBAD có
AM,DC là đường cao
AM cắt DC tại H
=>H là trực tâm
=>BH vuông góc AD
mà BH vuông góc AH(H nằm trên đường tròn đường kính AB)
nên A,H,D thẳng hàng

\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)

a: \(\widehat{B}=\dfrac{180^0-80^0}{2}=50^0\)
b: Chiều dài là \(\sqrt{15^2-9^2}=12\left(dm\right)\)

5: \(=\dfrac{1}{2}\cdot10-\dfrac{1}{2}=\dfrac{1}{2}\cdot9=\dfrac{9}{2}\)

a. f(\(\dfrac{-1}{2}\)) = \(4.\left(\dfrac{-1}{2}\right)^2+3.\left(\dfrac{-1}{2}\right)-2\)
= \(4.\dfrac{1}{4}-\left(\dfrac{-3}{2}\right)-\dfrac{4}{2}\)
= \(\dfrac{2}{2}+\dfrac{3}{2}-\dfrac{4}{2}\)
= \(\dfrac{1}{2}\)

4) \(\left|\dfrac{5}{18}-x\right|-\dfrac{7}{24}=0\)
\(\Leftrightarrow\left|\dfrac{5}{18}-x\right|=\dfrac{7}{24}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{5}{18}-x=\dfrac{7}{24}\\\dfrac{5}{18}-x=-\dfrac{7}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{72}\\x=\dfrac{41}{72}\end{matrix}\right.\)
b) \(\dfrac{2}{5}-\left|\dfrac{1}{2}-x\right|=6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=-\dfrac{28}{5}\)( vô lý do \(\left|\dfrac{1}{2}-x\right|\ge0\forall x\))
Vậy \(S=\varnothing\)

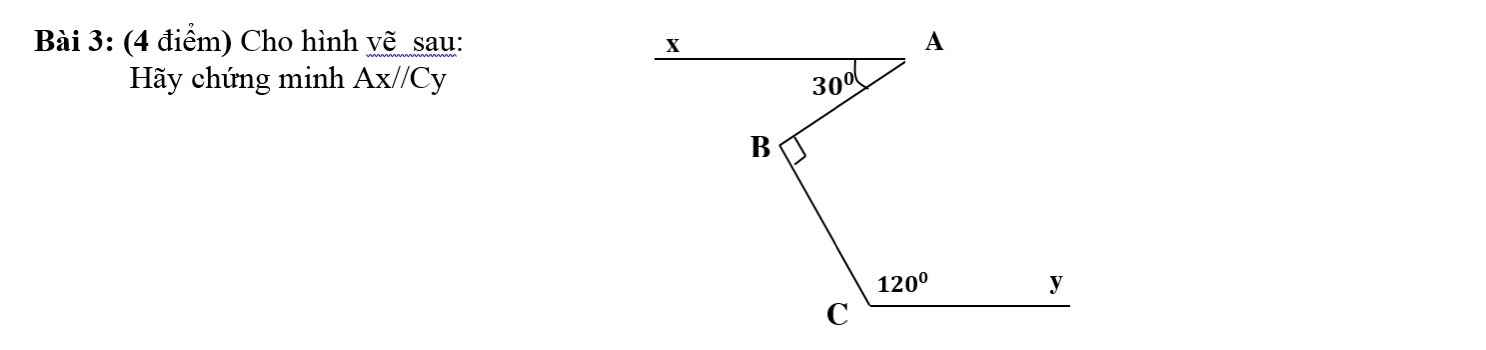
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
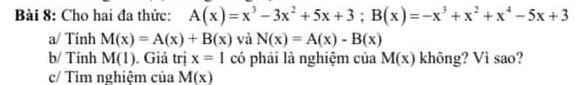 giúp mik với ạ, mik đang cần gấp><
giúp mik với ạ, mik đang cần gấp><

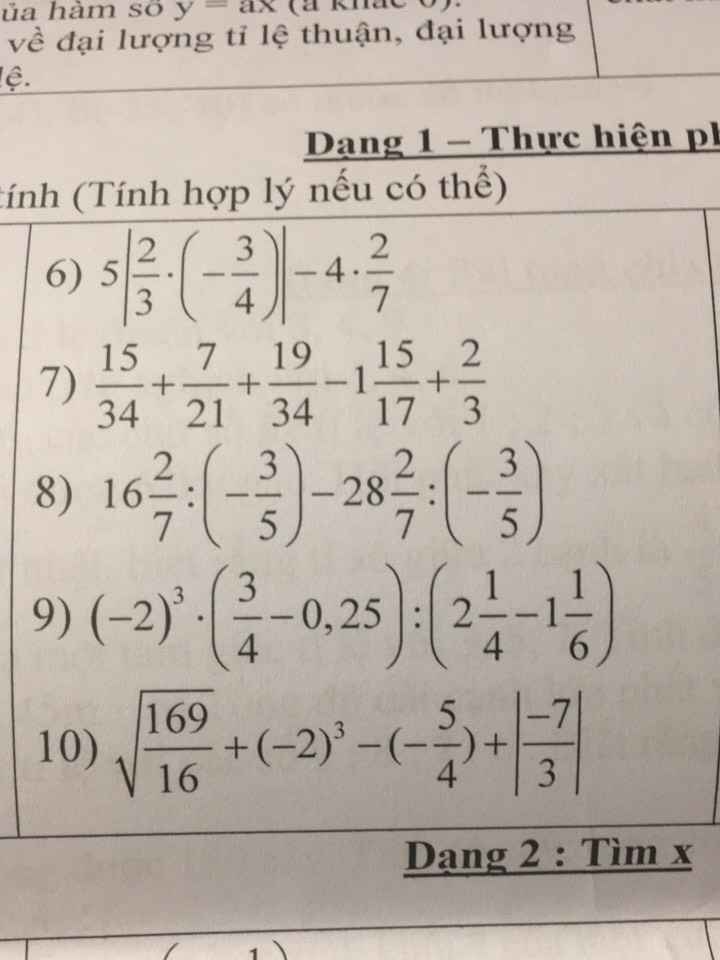

`8,`
`a,`
`M(x)=A(x)+B(x)`
`M(x)=(x^3-3x^2+5x+3)+(-x^3+x^2+x^4-5x+3)`
`= x^3-3x^2+5x+3-x^3+x^2+x^4-5x+3`
`= x^4+ (x^3-x^3)+(-3x^2+x^2)+(5x-5x)+(3+3)`
`= x^4-2x^2+6`
`N(x)=A(x)-B(x)`
`N(x)=(x^3-3x^2+5x+3)-(-x^3+x^2+x^4-5x+3)`
`= x^3-3x^2+5x+3+x^3-x^2-x^4+5x-3`
`= x^4+(x^3+x^3)+(-3x^2-x^2)+(5x+5x)+(3-3)`
`= x^4+2x^3-4x^2+10x`
`b,`
Thay `x=1`
`M(1)=1^4-2*1^2+6=1-2+6=-1+6=5`
`-> x=1` không phải là nghiệm của đa thức.
`c,`
`M(x)=x^4-2x^2+6=0`
\(\text{Vì }\)\(x^4\ge0\text{ }\forall\text{ }x\)
`-> x^4-2x^2+6 >0 AA x`
`->` Đa thức vô nghiệm.
a)\(M\left(x\right)=x^3-3x^2+5x+3-x^3+4x^2+x^4-5x+3\\ =x^4+x^2+6\)
\(N\left(x\right)=x^3-3x^2+5x+3+x^3-4x^2-x^4+5x-3\\ =-x^4+2x^3-7x^2+10x\)
b) \(M\left(1\right)=1^4+1^2+6=8\ne0\)
=> x=1 ko phai la nghiem M(x)
c) De M(x) co nghiem
\(x^4+x^2+6=0\)
vi \(x^4\ge0\forall x\\ x^2\ge0\forall x\\ \Rightarrow x^4+x^2+6\ge6\)
=> vo nghiem