
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ∆ ABC cân tại A (gt). \(\Rightarrow\) AB = AC (Tính chất tam giác cân).
Mà AB = BM (gt).
\(\Rightarrow\) AB = AC = BM.
Xét tứ giác ACMB:
BM = AC (cmt).
BM // AC (Bx // AC).
\(\Rightarrow\) Tứ giác ACBM là hình bình hành (dhnb).
Mà AB = BM (gt).
\(\Rightarrow\) Tứ giác ACBM là hình thoi (dhnb).
\(\Rightarrow\) \(AM\perp BC\) (Tính chất hình thoi).
b) Xét ∆ MBC:
MB = MC (Tứ giác ACBM là hình thoi).
\(\Rightarrow\) ∆ MBC cân tại M.

a: Xét ΔABM và ΔADM có
AB=AD
\(\widehat{BAM}=\widehat{DAM}\)
AM chung
Do đó;ΔABM=ΔADM
b:
Xét ΔAKD và ΔACB có
\(\widehat{ADK}=\widehat{ABC}\)
AD=AB
\(\widehat{DAK}\) chung
Do đó: ΔAKD=ΔACB
Suy ra: AK=AC
hay ΔAKC cân tại A
c: Xét ΔABC có AM là phân giác
nên BM/AB=CM/AC
mà AB<AC
nên BM<CM


Có: 7-3.\(\frac{-1}{4}^2\)
= 7-3. \(\frac{1}{16}\)
= 7- \(\frac{3}{16}\)
= \(\frac{112}{16}\)-\(\frac{3}{16}\)
= \(\frac{109}{16}\)

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O

\(c,\Rightarrow\left|x-\dfrac{1}{9}\right|=-\dfrac{4}{5}\\ \Rightarrow x\in\varnothing\left(\left|x-\dfrac{1}{9}\right|\ge0>-\dfrac{4}{5}\right)\\ d,\Rightarrow\left\{{}\begin{matrix}3x-2=0\\4y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{7}{4}\end{matrix}\right.\\ e,\Rightarrow\left\{{}\begin{matrix}2x+1=0\\x-y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\x=y=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x=y=-\dfrac{1}{2}\)

\(1,=5\dfrac{1}{4}\left(-6\dfrac{12}{27}-1\dfrac{5}{17}\right)=\dfrac{21}{4}\left(-\dfrac{1184}{153}\right)=-\dfrac{2072}{51}\\ 2,=\left(-\dfrac{3}{4}\cdot\dfrac{4}{5}\right)^2+\dfrac{147}{10}-\dfrac{34}{25}=\dfrac{9}{25}-\dfrac{34}{25}+\dfrac{147}{10}=\dfrac{147}{10}-1=\dfrac{137}{10}\)
 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ


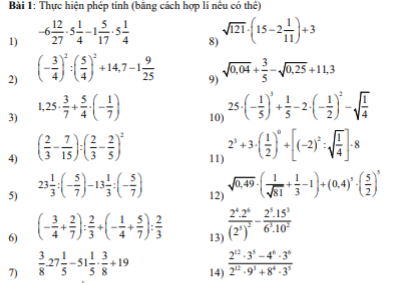 giúp mik với ạ mik cần gấp
giúp mik với ạ mik cần gấp
Bạn đăng câu hỏi lên nhé .-.