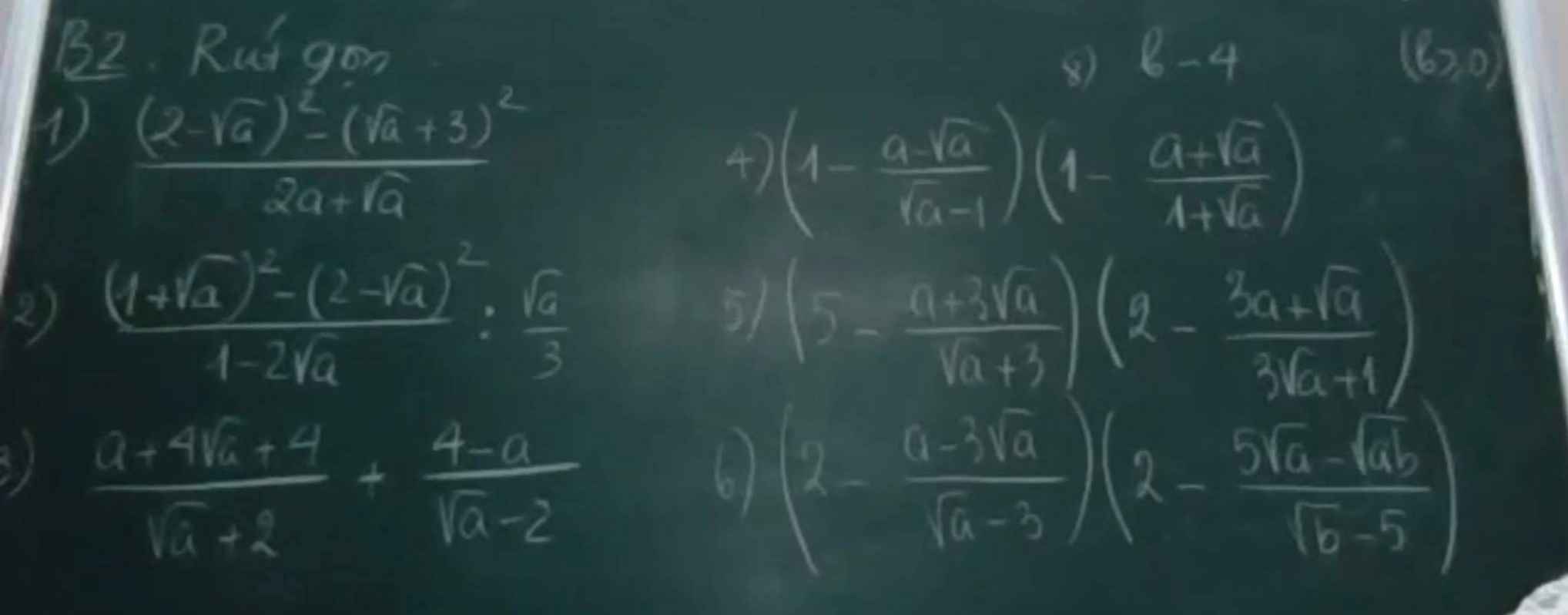Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ủa r siêng năng may vượt mức chi r để hs phải đi tính zị trời😤

\(b,\text{PT hoành độ giao điểm: }-2x=3x+3\\ \Leftrightarrow x=-\dfrac{3}{5}\Leftrightarrow y=\dfrac{6}{5}\\ \Leftrightarrow A\left(-\dfrac{3}{5};\dfrac{6}{5}\right)\)

\(11,=\dfrac{\sqrt{10}}{5}=\dfrac{1}{5}\sqrt{10}\left(A\right)\\ 12,=\dfrac{2\left(\sqrt{5}+3\right)}{-4}=-\dfrac{\sqrt{5}+3}{2}\left(B\right)\\ 13,=\dfrac{\sqrt{a}}{3\sqrt{3}}=\dfrac{\sqrt{3a}}{9}\left(A\right)\\ 14,B\)


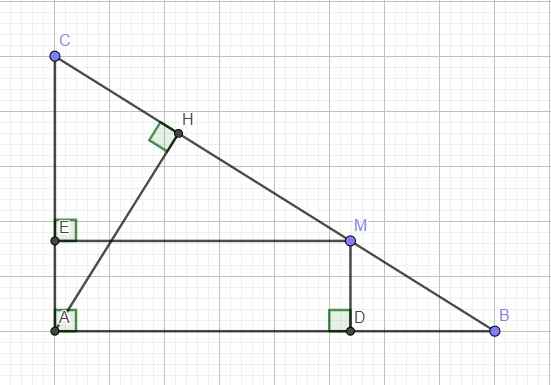
Theo giả thiết: \(ME\perp AC\Rightarrow\Delta MEA\) vuông tại E \(\Rightarrow\) E thuộc đường tròn đường kính AM (1)
Tương tự, tam giác MDA vuông tại D \(\Rightarrow\) D thuộc đường tròn đường kính AM (2)
Tam giác MHA vuông tại H \(\Rightarrow\) H thuộc đường tròn đường kính AM (3)
(1);(2);(3) \(\Rightarrow\) 5 điểm A, D, M, H, E cùng thuộc đường tròn đường kính AM (đpcm)

2) \(\dfrac{\left(1+\sqrt{a}\right)^2-\left(2-\sqrt{a}\right)^2}{1-2\sqrt{a}}:\dfrac{\sqrt{a}}{3}\left(a>0,a\ne\dfrac{1}{4}\right)\)
\(=\dfrac{\left(1+\sqrt{a}-2+\sqrt{a}\right)\left(1+\sqrt{a}+2-\sqrt{a}\right)}{1-2\sqrt{a}}.\dfrac{3}{\sqrt{a}}\)
\(=\dfrac{3.\left(2\sqrt{a}-1\right)}{1-2\sqrt{a}}.\dfrac{3}{\sqrt{a}}=-\dfrac{9}{\sqrt{a}}\)
5) \(\left(5-\dfrac{a+3\sqrt{a}}{\sqrt{a}+3}\right)\left(2-\dfrac{3a+\sqrt{a}}{3\sqrt{a}+1}\right)\left(a\ge0\right)\)
\(=\left(5-\dfrac{\sqrt{a}\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\right)\left(2-\dfrac{\sqrt{a}\left(3\sqrt{a}+1\right)}{3\sqrt{a}+1}\right)\)
\(=\left(5-\sqrt{a}\right)\left(2-\sqrt{a}\right)=10-7\sqrt{a}+a\)
6) \(\left(2-\dfrac{a-3\sqrt{a}}{\sqrt{a}-3}\right)\left(2-\dfrac{5\sqrt{a}-\sqrt{ab}}{\sqrt{b}-5}\right)\left(a,b\ge0,a\ne9,b\ne25\right)\)
\(=\left(2-\dfrac{\sqrt{a}\left(\sqrt{a}-3\right)}{\sqrt{a}-3}\right)\left(2+\dfrac{\sqrt{a}\left(\sqrt{b}-5\right)}{\sqrt{b}-5}\right)\)
\(=\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)=4-a\)
3) Ta có: \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\)
\(=\sqrt{a}+2-\sqrt{a}-2\)
=0

Câu 3:
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)





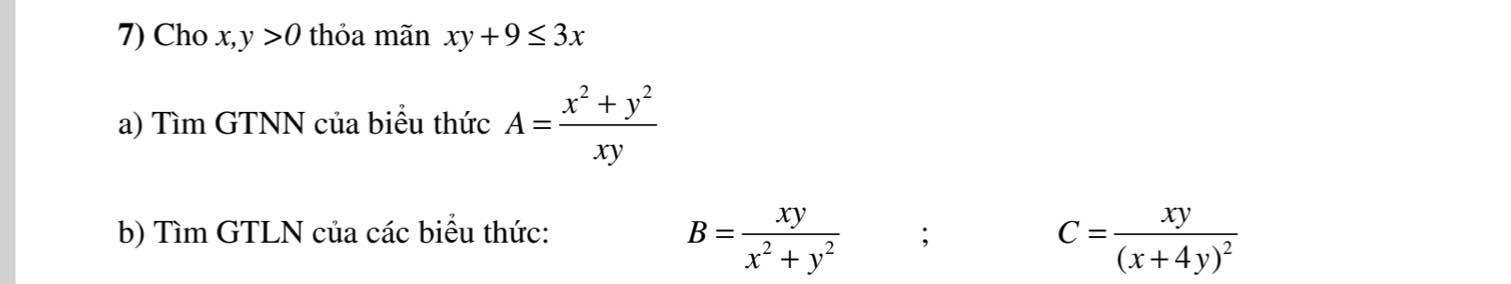 mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺
mọi người giúp em 2 ý này với ạ, em rất cảm ơn ạ 🥺 mọi người giúp em với ạ 🥺
mọi người giúp em với ạ 🥺