K
Khách
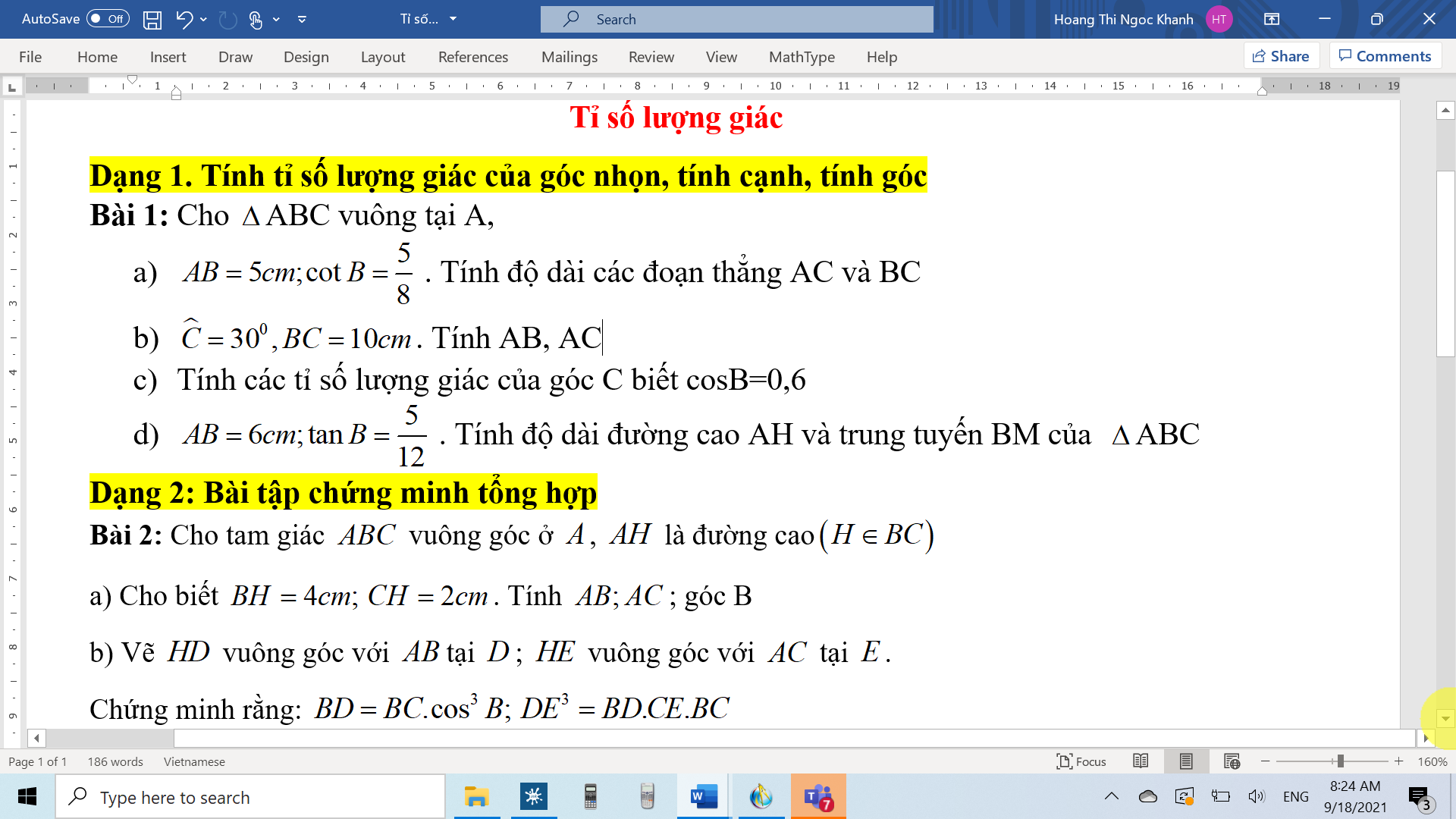
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 12 2020
a. \(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}=\dfrac{\sqrt{3}-1}{1-\sqrt{3}}=-1\)
b. \(\dfrac{3}{\sqrt{2}-1}-\dfrac{3}{\sqrt{2}+1}\)
\(=\dfrac{3\left(\sqrt{2}+1\right)}{2-1}-\dfrac{3\left(\sqrt{2}-1\right)}{2-1}\)
\(=3\sqrt{2}+3-3\sqrt{2}+3\)
\(=6\)
15 tháng 6 2023
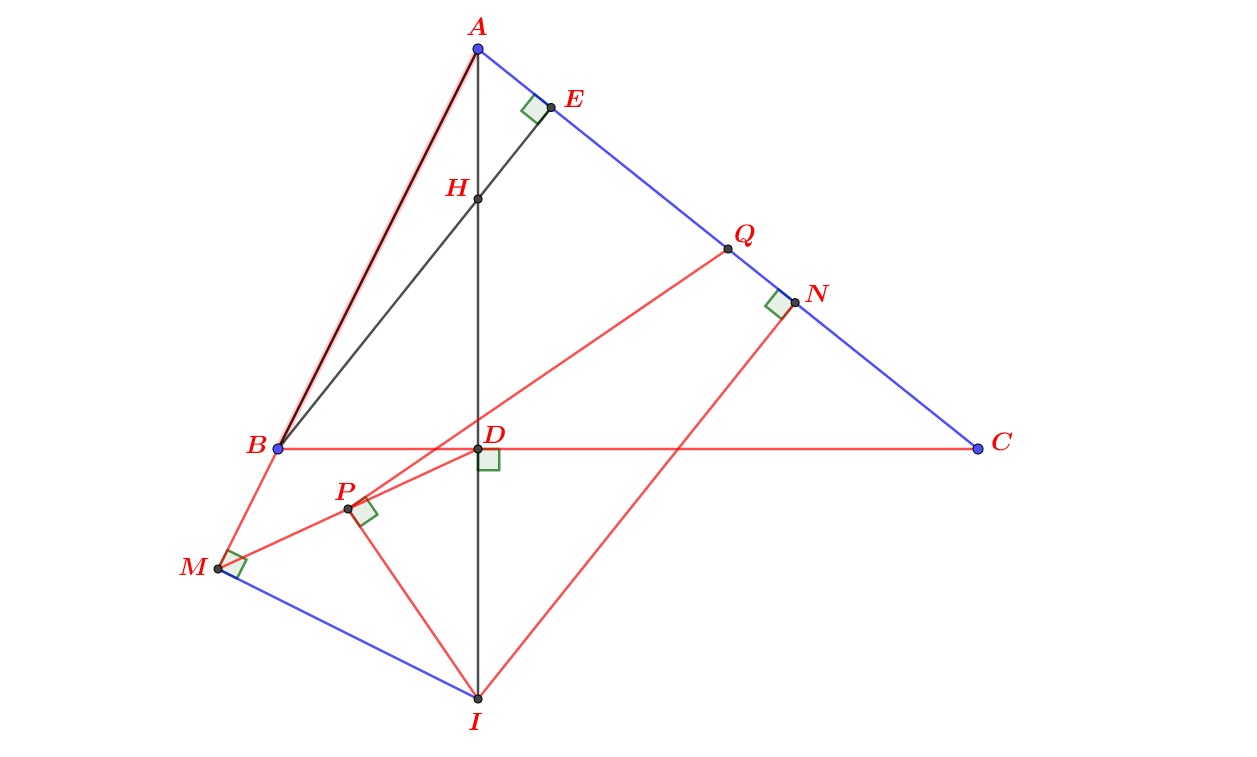
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
c: H đối xứng P qua D
=>DH=DP
Xét ΔBHP có
BD vừa là đường cao, vừa là trung tuyến
=>ΔBHP cân tại B
=>BH=BP và góc HBC=góc PBC
Xét ΔBHC và ΔBPC có
BH=BP
góc HBC=góc PBC
BC chung
=>ΔBHC=ΔBPC
=>góc BPC=góc BHC
=>góc BPC+góc BAC=180 độ
=>P thuộc (O)
22 tháng 4 2020
a)Tam giác MAO vuông tại A
=> MO2 = AO2 + AM2
=> 72 = 52 + AM2
=> AM2 = 24
=> AM = \(2\sqrt{6}\)(cm)
b) Ta có:
OM - ON = MN
=> MN = 7-5 = 2(cm)
=> MP = OP + OM = 5 + 7 = 12 (cm)
=> MP.MN = 12.2 = 24
MA2 = 24
Vậy MA2 = MP.MN
31 tháng 3 2022
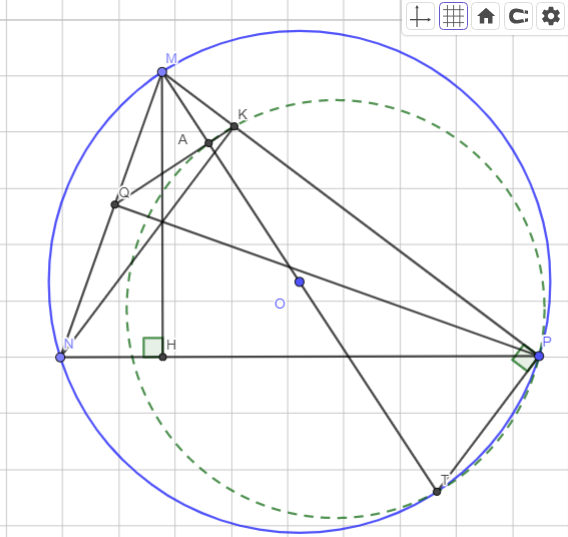
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình:
29 tháng 3 2022
Dạ bài anh có nhầm lẫn gì kh ạ chứ khúc đầu e thấy hơi sai sai 😅😅
b: Xét ΔMAN và ΔMPA có
góc MAN=góc MPA
góc AMN chung
=>ΔMAN đồng dạng với ΔMPA
=>MA/MP=MN/MA
=>MA^2=MN*MP