K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LC
0
15 tháng 11 2021
\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
VT
3
21 tháng 10 2021
Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)
NT
2
6 tháng 9 2021
\(B=\left(x^2+x\right)^2+4\left(x^2+x\right)+4-16=\left(x^2+x+2\right)^2-16\ge-16\)
Dấu \("="\Leftrightarrow x^2+x+2=0\Leftrightarrow x\in\varnothing\left(x^2+x+2>0\right)\)
Vậy dấu \("="\) ko xảy ra nên sẽ ko tính đc GTNN
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
1.
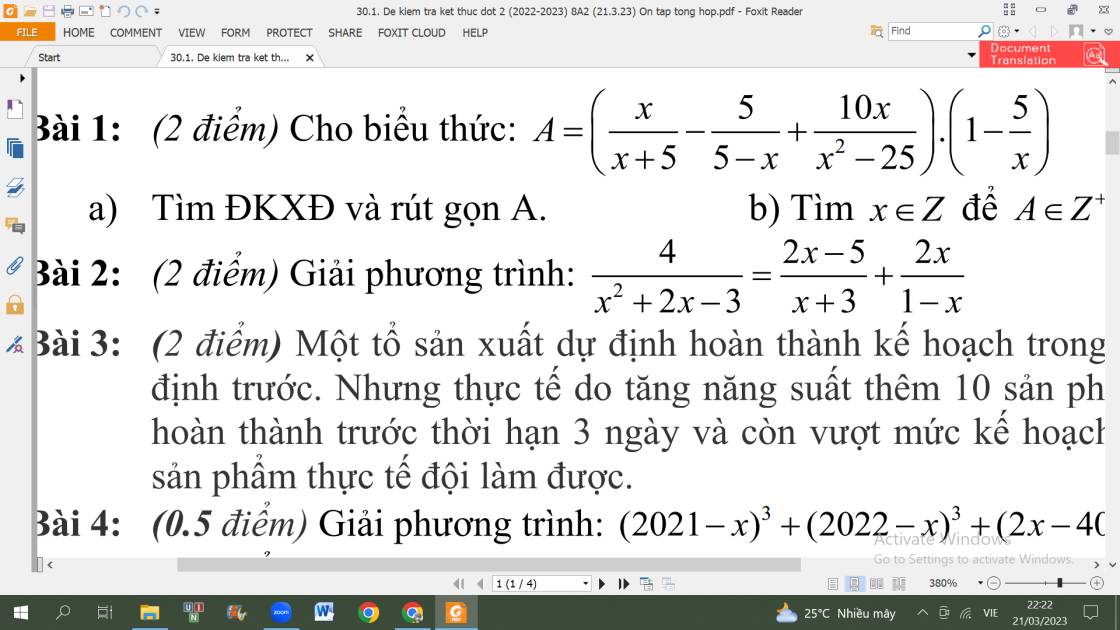
a. ĐKXĐ: \(x\ne\left\{0;-5;5\right\}\)
\(A=\left(\dfrac{x}{x+5}+\dfrac{5}{x-5}+\dfrac{10x}{x^2-25}\right).\left(1-\dfrac{5}{x}\right)\)
\(=\left(\dfrac{x\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}+\dfrac{5\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}+\dfrac{10x}{\left(x-5\right)\left(x+5\right)}\right).\left(\dfrac{x-5}{x}\right)\)
\(=\left(\dfrac{x^2-5x+5x+25+10x}{\left(x-5\right)\left(x+5\right)}\right)\left(\dfrac{x-5}{x}\right)\)
\(=\left(\dfrac{x^2+10x+25}{\left(x-5\right)\left(x+5\right)}\right)\left(\dfrac{x-5}{x}\right)\)
\(=\dfrac{\left(x+5\right)^2\left(x-5\right)}{\left(x-5\right)\left(x+5\right).x}=\dfrac{x+5}{x}\)
b.
\(A=\dfrac{x+5}{x}=1+\dfrac{5}{x}\)
\(A\in Z\Rightarrow\dfrac{5}{x}\in Z\Rightarrow5⋮x\)
\(\Rightarrow x=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
Thay vào ta được \(A=\left\{0;-4;6;2\right\}\)
Do A nguyên dương nên loại \(A=\left\{0;-4\right\}\) tương ứng \(x=\left\{-5;-1\right\}\)
Vậy \(x=\left\{1;5\right\}\)
21 tháng 3 2023
2:
=>4=(2x-5)(x-1)-2x(x+3)
=>2x^2-2x-5x+5-2x^2-6x=4
=>-13x+5=4
=>-13x=-1
=>x=1/13
29 tháng 5 2022
Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B
Giúp e bài hình với ạ.
Bài 2:
Xé ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành