Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A.
Ta thấy phương trình x 2 - b x + b - 1 = 0 có a + b + c = 0 nên có nghiệm x 1 = 1 , x 2 = b - 1 .
Vậy để phương trình có nghiệm lớn hơn 3 thì b - 1 > 3 ⇔ b > 4 ⇒ b ∈ 5 ; 6 .
Do đó xác suất để phương trình có nghiệm lớn hơn 3 là 2 6 = 1 3 . Ta chọn A.

Đáp án A.
Ta thấy phương trình x 2 − b x + b − 1 = 0 có a + b + c = 0 nên có nghiệm x 1 = 1, x 2 = b − 1 .
Vậy để phương trình có nghiệm lớn hơn 3 thì b − 1 > 3 ⇔ b > 4 ⇒ b ∈ 5 ; 6 .
Do đó xác suất để phương trình có nghiệm lớn hơn 3 là 2 6 = 1 3 . Ta chọn A.

Đáp án D.
Phương trình x 2 + b x + 2 = 0 có hai nghiệm phân biệt ⇔ Δ = b 2 − 8 > 0.
Mà 1 ≤ b ≤ 6 , b ∈ ℕ * ⇒ b ∈ 3 ; 4 ; 5 ; 6 .
Xác suất cần tìm là 4 6 = 2 3 .

Đáp án C
Có 6 khả năng xảy ra khi tung súc sắc nên số phần tử của không gian mẫu là n ( Ω ) = 6 .
Gọi A là biến cố: Phương trình x 2 + b x + 2 = 0 (1) có hai nghiệm phân biệt.
Phương trình (1) có hai nghiệm phân biệt ⇔ b 2 − 8 > 0 ⇔ b ∈ 3 ; 4 ; 5 ; 6 ⇒ n A = 4 .
Vậy xác suất cần tính là p A = 2 3 .

Đáp án C
Số phần tử không gian mẫu là 6 3 = 216.
Các bộ ba số lập thành một cấp số cộng là ( 1 , 2 , 3 ) , ( 2 , 3 , 4 ) , ( 3 , 4 , 5 ) , ( 4 , 5 , 6 ) . Bốn trường hợp trên với các hoán vị sẽ có 4 ⋅ 6 .
Xác suất cần tìm là 24 216 = 1 9 .

Chọn B.
Phương pháp:
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: "Hiệu số chấm xuất hiện trên các mặt của hai con súc sắc bằng 2". Tìm đẩy đủ các bộ số có hiệu bằng 2.
+) Tính xác suất của biến cố A.
Cách giải:
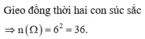
Gọi A là biến cố: "Hiệu số chấm xuất hiện trên các mặt của hai con súc sắc bằng 2".
Các bộ số có hiệu bằng 2 là (1;3); (2;4); (3;5); (4;6)