K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
21 tháng 1 2019
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
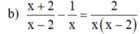
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
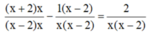
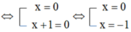
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
CM
10 tháng 2 2018
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
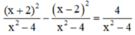
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
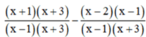
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
PN
15 tháng 5 2021
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
CM
29 tháng 11 2017
Điều kiện xác định: x ≠ 2.
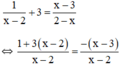
Suy ra: 1 + 3(x – 2) = -(x – 3)
⇔ 1 + 3x – 6 = -x + 3
⇔ 3x + x = 3 + 6 – 1
⇔ 4x = 8
⇔ x = 2 (không thỏa mãn đkxđ).
Vậy phương trình vô nghiệm.
CM
31 tháng 3 2019
a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
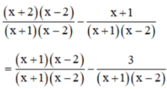
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.
CM
16 tháng 3 2018
a) 8( 3x - 2 ) - 14x = 2( 4 – 7x ) + 15x
⇔ 24x – 16 -14x = 8 – 14x + 15x
⇔ 10x -16 = 8 + x
⇔ 9x = 24
⇔ x = 24/9
b) ( 3x – 1 )( x – 3 ) – 9 + x2 = 0
⇔ (3x -1)( x – 3) + (x - 3)( x + 3) = 0
⇔ (x - 3)(3x - 1 + x - 3) = 0
⇔ (x - 3)(4x - 4) = 0
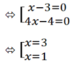
c) |x - 2| = 2x - 3
TH1: x - 2 ≥ 0 ⇔ x ≥ 2
Khi đó: x - 2 = 2x – 3
⇔ 2x – x = -2 + 3
⇔ x = 1 (không TM điều kiện x ≥ 2)
TH2: x – 2 < 0 ⇔ x < 2
Khi đó: x-2 = -(2x – 3)
⇔ x – 2 = -2x + 3
⇔ 3x = 5
⇔ x = 5/3 ( TM điều kiện x < 2)
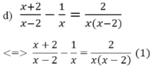
MTC: x(x-2)
ĐKXĐ: x ≠ 0;x ≠ 2
Đối chiếu với ĐKXĐ thì pt có nghiệm x = - 1
CM
30 tháng 11 2017
ĐKXD: x ≠ {2, 3, 4, 5}
Phương trình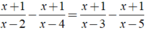
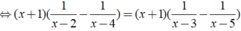
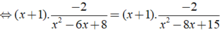
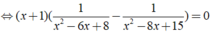
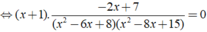
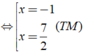
Vậy nghiệm của phương trình là x = - 1;x = 7/2
Chọn đáp án C.
lắm dấu = z?
x(x+3)²=(x+2)³+1
⇔x(x²+6x+9)=x³+3.x².2+3.x.4+2³+1
⇔x³+6x²+9x=x³+6x²+12x+8+1
⇔x³+6x²+9x-x³-6x²-12x=9
⇔-3x=9
⇔x=-3