LD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 2 2023
a: \(\Leftrightarrow\dfrac{y+5}{y\left(y-5\right)}-\dfrac{y-5}{2y\left(y+5\right)}=\dfrac{y+25}{2\left(y-5\right)\left(y+5\right)}\)
\(\Leftrightarrow2\left(y+5\right)^2-\left(y-5\right)^2=y^2+25y\)
=>\(2y^2+20y+50-y^2+10y-25=y^2+25y\)
=>30y+25=25y
=>5y=-25
=>y=-5(loại)
b: \(\Leftrightarrow x\left(x+1\right)+x\left(x-3\right)=4x\)
=>x^2+x+x^2-3x-4x=0
=>2x^2-6x=0
=>2x(x-3)=0
=>x=0(nhận) hoặc x=3(loại)
c: =>x^2-9-6(2x+7)=-13(x+3)
=>x^2-9-12x-42+13x+39=0
=>x^2+x-6=0
=>(x+3)(x-2)=0
=>x=2(nhận) hoặc x=-3(loại)
CV
1
9 tháng 1 2021
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
9 tháng 1 2021
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
CM
19 tháng 1 2019
Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
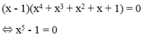
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.
LM
3
22 tháng 12 2021
\(2x^2-4xy+2y^2\\ =2\left(x^2-2xy+y^2\right)\\ =2\left(x-y\right)^2\)
22 tháng 12 2021
a) 2x2-4xy+2y2
= 2x2-2xy-2xy+2y2
= 2x(x-y)-2y(x-y)
= (2x-2y)(x-y)
b) x2+4xy+4y2-9
= (x+2y)2-32
= (x+2y-3)(x+2y+3)
c) x4-x3y+x-y
= x3(x-y)+(x-y)
= (x3+1)(x-y)
x4 - 2y2 = 1 => x4 - 1 = 2y2 ( 1 )
Dễ thấy : x lẻ \(x^4\equiv1\) ( mod 4 )
=> y2 chẵn => y chẵn
Đặt \(x=2k+1;y=2n\left(k;n\in Z\right)\). Ta có :
\(\left(4k^2+4k+1\right)^2-1=8n^2\)
\(\Leftrightarrow\left(4k^2+4k+2\right)\left(4k^2+4k\right)=8n^2\)
\(\Leftrightarrow\left(2k^2+2k+1\right)\left(k^2+k\right)=n^2\)
Với k = 0 thì \(y=0\) ( tm )
Thay y = 0 vào ( 1 ) ta được \(x=\pm1\) ( tm )
Với \(k\ge1\)
Đặt \(k^2+k=m\)
\(\Rightarrow\left(2m+1\right)m=n^2\)
=> m ; 2m + 1 là SCP
Ta lại có : \(k^2< k^2+k< \left(k+1\right)^2\)
Vì k2 + k kẹp giữa 2 SCP liên tiếp nên k2 + k không thể là SCP
Vậy pt có các nghiệm ( x ; y ) là : ( 1 ; 0 ) ; ( - 1 ; 0 )
Tohru ( ʚ๖ۣۜTεαм ๖ۣۜFℓαʂɦɞ ) làm vậy có dài không bạn?
\(x^4-2y^2=1\Leftrightarrow x^4=1+2y^2\)
Do \(\hept{\begin{cases}x^4\ge0\forall x\\2y^2\ge0\forall y\end{cases}}\)
Để x,y nguyên => \(\hept{\begin{cases}x^4=1\\2y^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\pm1\\y=0\end{cases}}}\)