PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
PT
1
CM
30 tháng 12 2019
2 cos 2 x - 3 sin 2 x + sin 2 x = 1
- cosx = 0 thỏa mãn phương trình ⇒ phương trình có nghiệm x = π/2+kπ,k ∈ Z.
- Với cosx ≠ 0, chia hai vế cho cos 2 x , tìm được tanx = 1/6.
Vậy phương trình có các nghiệm x = π/2+kπ,k ∈ Z và x = arctan1/6 + kπ,k ∈ Z.
CM
5 tháng 8 2018
Hướng dẫn giải:
Chọn A.
+ Trường hợp 1.
: là nghiệm của phương trình
+ Trường hợp 2.
: Chia 2 vế phương trình cho cos2x ta được
CM
16 tháng 2 2017
cos 2 x = 3 sin 2 x + 3
Ta thấy cosx = 0 không thỏa mãn phương trình. Với cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:
21 tháng 7 2022
a: \(\sqrt{3^2+2^2}=\sqrt{13}\)
Chia hai vế cho căn 13, ta được:
\(\dfrac{3}{\sqrt{13}}\cdot\sin2x+\dfrac{2}{\sqrt{13}}\cdot\cos2x=\dfrac{3}{\sqrt{13}}\)
Đặt \(\cos a=\dfrac{3}{\sqrt{13}}\)
Ta được phương trình: \(\sin\left(2x+a\right)=\cos a=\sin\left(\dfrac{\Pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+a=\dfrac{\Pi}{2}-a+k2\Pi\\2x+a=\dfrac{\Pi}{2}+a+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\left(\dfrac{\Pi}{2}-2a+k2\Pi\right)\\x=\dfrac{\Pi}{4}+k\Pi\end{matrix}\right.\)
b: \(\Leftrightarrow cos^2x-sin^2x+cosx-sinx=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x=\cos\left(\dfrac{\Pi}{2}-x\right)\\\sin\left(x-\dfrac{\Pi}{4}\right)=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{2}-x+k2\Pi\\x=-\dfrac{\Pi}{2}+x+k2\Pi\\x-\dfrac{\Pi}{4}=-\dfrac{\Pi}{2}+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{4}+k\Pi\\x=-\dfrac{\Pi}{4}+k2\Pi\end{matrix}\right.\)
PT
1
PT
1
CM
2 tháng 5 2018
4 cos 2 x - 3 sin x . cos x + 3 sin 2 x = 1
Rõ ràng cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:
4 - 3 tan x + 3 tan 2 x = 1 + tan 2 x ⇔ 2 tan 2 x - 3 tan x + 3 = 0
Phương trình cuối vô nghiệm đối với tanx, do đó phương trình đã cho vô nghiệm
25 tháng 8 2021
Điều kiện xác định : sin4x ≠ 0
3tan2x + 2cos2x = \(\dfrac{3}{cos2x}\) + 2 \(\dfrac{sin\left(x-\dfrac{\pi}{4}\right)}{cos\left(x-\dfrac{\pi}{4}\right)}\)
⇔ 3tan2x + 2cos2x = \(\dfrac{3}{cos2x}\) + 2 \(\dfrac{sinx-cosx}{sinx+cosx}\)
⇒ 3tan2x . cos2x + 2cos22x = 3 + 2\(\dfrac{sinx-cosx}{sinx+cosx}\).cos2x
⇒ 3sin2x + 2cos22x = 3 + 2. \(\dfrac{sinx-cosx}{sinx+cosx}\).(cosx - sinx)(cosx + sinx)
⇒ 3sin2x + 2cos22x = 3 - 2(sinx - cosx)2
⇔ 3sin2x + 2cos22x = 3 - 2 . (1 - sin2x)
⇔ 3sin2x + 2 - 2sin22x = 3 - 2 + 2sin2x
⇔ - 2sin22x + sin2x + 1 = 0
⇔ \(\left[{}\begin{matrix}sin2x=1\\sin2x=-\dfrac{1}{2}\end{matrix}\right.\)
Loại sin2x = 1 vì khi đó cos2x = 0 (vi phạm ĐKXĐ)
⇔ sin2x = \(-\dfrac{1}{2}\)
Giải nốt nhé
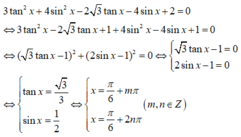
Vậy phương trình có tập nghiệm