Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: =>(x^2-2x+1-1)^2+2(x-1)^2=1
=>(x-1)^4-2(x-1)^2+1+2(x-1)^2=1
=>(x-1)^4=0
=>x-1=0
=>x=1
b: =>(x^2+2)^2+3x(x^2+2)+2x^2-20x^2=0
=>(x^2+2)^2+3x(x^2+2)-18x^2=0
=>(x^2+2+6x)(x^2-3x+2)=0
=>\(x\in\left\{-3\pm\sqrt{7};1;2\right\}\)

Mình nghĩ đề câu a là: \(x+\sqrt{5}+\sqrt{x}-1=-6\)
Đặt \(\sqrt{x}=t\Rightarrow t^2=x\)
\(Ta\)\(được\): \(t^2+\sqrt{5}+t-1=-6\)
\(\Leftrightarrow t^2-5+t+\sqrt{5}=0\)
\(\Leftrightarrow\left(t-\sqrt{5}\right).\left(t+\sqrt{5}\right)+\left(t+\sqrt{5}\right)=0\)
\(\Leftrightarrow\left(t+\sqrt{5}\right).\left(t-\sqrt{5}+1\right)=0\)
\(\Rightarrow\hept{\begin{cases}t=-\sqrt{5}\\t=\sqrt{5}-1\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=5\\x=6-2\sqrt{5}\end{cases}}\)

Nếu đặt u = x 2 − 1 thì x 2 = u + 1 nên phương trình có dạng
( 2 + 2)u = 2(u + 1) − 2 (1)
Ta giải phương trình (1):
(1) ⇔ 2 u + 2u = 2u + 2 − 2
⇔ 2 u = 2 − 2
⇔ 2 u = 2 ( 2 − 1) ⇔ u = 2 − 1
⇔ x 2 − 1 = 2 − 1
⇔ x 2 = 2
⇔ x = 1

\(|x-6|=-5x+9\)
Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)
\(< =>x-6+5x-9=0\)
\(< =>6x-15=0\)
\(< =>x=\frac{15}{6}\)(ktm)
Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)
\(< =>4x-9+6=0\)
\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)
Vậy ...
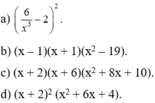

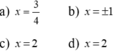
2/ (x2 + x + 1) (x2+ x + 2) = 12
đặt x2 + x = t
thay vào đc:
(t + 1) (t + 2) = 12
<=> t2 + 3t + 2 = 12
<=> t2 + 3t - 10 = 0
<=> t2 - 2t + 5t - 10 = 0
<=> t (t - 2) + 5 (t - 2) = 0
<=> (t + 5) (t - 2) = 0
=> {
t=−5
t=2
thay t đc:
*) x2 + x = -5 => x loại
*) x2 + x = 2 = x2 + x - 2 = x2 - 1 + x - 1 = (x - 1) (x + 1) + (x - 1) = (x - 1) (x + 2)
=> x = 1 hoặc x = - 2
S = {-2 ; 1}
3/ (x2 - 6x + 4)2 - 15(x2 - 6x + 10) = 1
đặt x2 - 6x + 4 = t
có: t2 - 15(t + 6) = 1
<=> t2 - 15t - 91 = 0
Câu 2 đặt ẩn phụ là x^2+x+2= a là đc
Câu 3 đặt ẩnphụ là x^2-6x+4= b là đc