
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 5:
\(y=1-\left(sin2x+cos2x\right)^3\)
\(=1-\left[\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right]^3\)\(=1-2\sqrt{2}.sin^3\left(2x+\dfrac{\pi}{4}\right)\)
Có \(-1\le sin\left(2x+\dfrac{\pi}{4}\right)\le1\)
\(\Leftrightarrow-1\le sin^3\left(2x+\dfrac{\pi}{4}\right)\le1\) \(\Leftrightarrow1+2\sqrt{2}\ge y\ge1-2\sqrt{2}\)
\(\Rightarrow y_{min}=1-2\sqrt{2}\Leftrightarrow sin\left(2x+\dfrac{\pi}{4}\right)=1\)\(\Leftrightarrow x=\dfrac{\pi}{8}+k\pi\left(k\in Z\right)\)
\(\Rightarrow y_{max}=1+2\sqrt{2}\Leftrightarrow sin\left(2x+\dfrac{\pi}{4}\right)=-1\)\(\Leftrightarrow x=\dfrac{-3\pi}{8}+k\pi\left(k\in Z\right)\)
Ý B
Câu 6: Hàm số có TXĐ: D=R
\(y=\sqrt{4-2sin^52x}-8\)
Có \(-1\le sin2x\le1\)
\(\Leftrightarrow-1\le sin^52x\le1\)
\(\Leftrightarrow2\ge-2sin^52x\ge-2\)
\(\Leftrightarrow\)\(\sqrt{6}-8\ge y\ge\sqrt{2}-8\)
Ý A
Câu 7: TXĐ: D=R
\(y=\dfrac{3}{3-\sqrt{1-cosx}}\)
Có \(-1\le cosx\le1\) \(\Leftrightarrow2\ge1-cosx\ge0\) \(\Leftrightarrow3-\sqrt{2}\ge3-\sqrt{1-cosx}\ge3\)
\(\Leftrightarrow\dfrac{3}{3-\sqrt{2}}\le y\le1\)
Vậy \(y_{min}=\dfrac{3}{3-\sqrt{2}}\Leftrightarrow x=\pi+k2\pi\) (k nguyên)
\(y_{max}=1\Leftrightarrow x=k2\pi\) (k nguyên)


Áp dụng công thức \(\left(\dfrac{1}{v}\right)'=\dfrac{-v'}{v^2}\)
Ta có \(y'=\dfrac{-\left(x^2+x-1\right)'}{\left(x^2+x-1\right)^2}=-\dfrac{\left(2x+1\right)}{\left(x^2+x-1\right)^2}\)

c.
\(\Leftrightarrow sin4x=sin\left(3x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=3x-\dfrac{\pi}{2}+k2\pi\\4x=\dfrac{3\pi}{2}-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}+k2\pi\\x=\dfrac{3\pi}{14}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
d.
\(\Leftrightarrow sin\left(2x+30^0\right)=sin\left(30^0+x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+30^0=30^0+x+k360^0\\2x+30^0=150^0-x+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k360^0\\x=40^0+k120^0\end{matrix}\right.\)
e.
\(\Leftrightarrow cos3x=-sinx\)
\(\Leftrightarrow cos3x=cos\left(\dfrac{\pi}{2}+x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{\pi}{2}+x+k2\pi\\3x=-\dfrac{\pi}{2}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
f.
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)\left(sin2x+cos5x\right)=0\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)\left(sin2x-sin\left(5x-\dfrac{\pi}{2}\right)\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x-\dfrac{\pi}{4}\right)=0\\sin\left(5x-\dfrac{\pi}{2}\right)=sin2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=k\pi\\5x-\dfrac{\pi}{2}=2x+k2\pi\\5x-\dfrac{\pi}{2}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\\x=\dfrac{3\pi}{14}+\dfrac{k2\pi}{7}\end{matrix}\right.\)




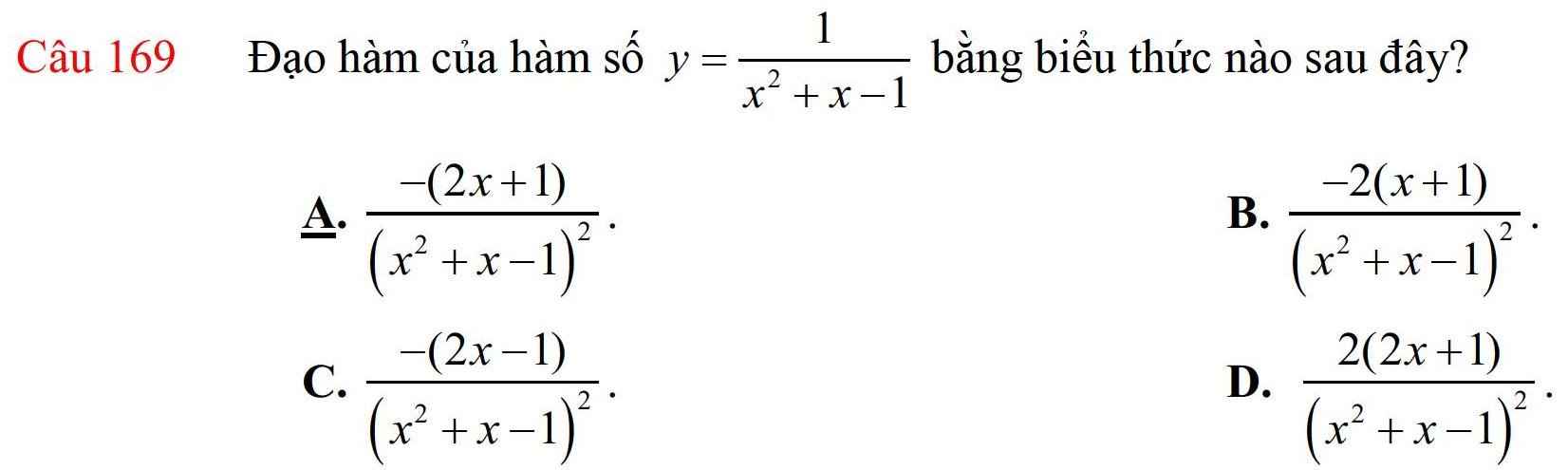
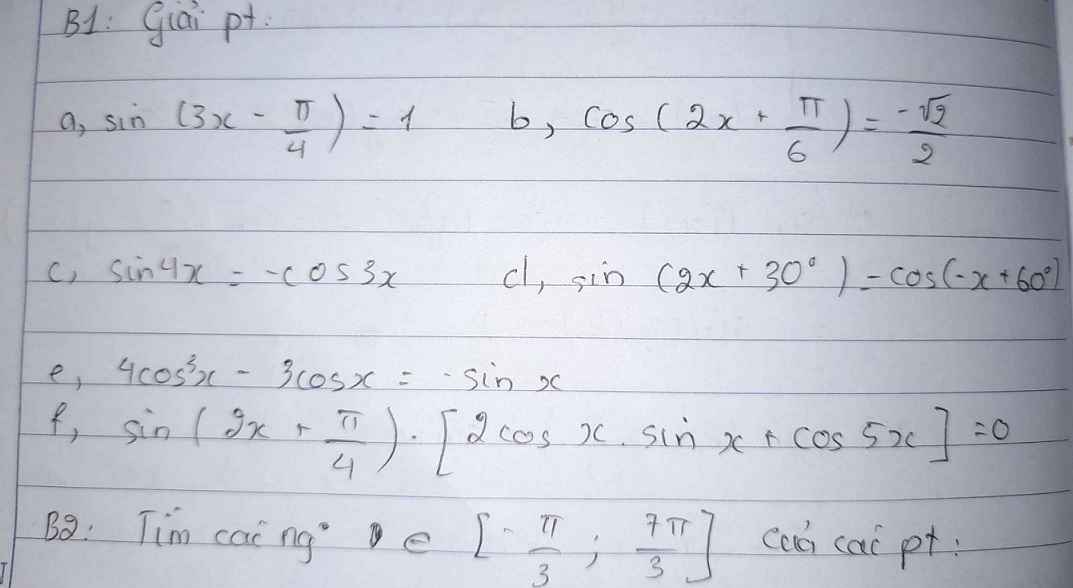
a.
Do \(-1\le sin2x\le1\) nên pt có nghiệm khi:
\(-1\le\dfrac{m+3}{2m-1}\le1\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m+3}{2m-1}+1\ge0\\\dfrac{m+3}{2m-1}-1\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3m+2}{2m-1}\ge0\\\dfrac{4-m}{2m-1}\le0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{2}{3}\\m\ge4\end{matrix}\right.\)
-1 ở đâu vậy ạ