TC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
11 tháng 5 2018
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
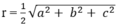
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
CM
8 tháng 2 2018
z 2 = ( a + b i ) 2 = a 2 − b 2 + 2abi
( z ) 2 = ( a - b i ) 2 = a 2 − b 2 − 2abi
z.z− = (a + bi)(a − bi) = a 2 + b 2
Từ đó suy ra các kết quả.
CM
9 tháng 12 2018
Đáp án D
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất
CM
26 tháng 3 2019
Đáp án D.
Ta có
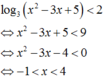
Suy ra a = - 1 , b = 4 Do đó a 2 + b 2 = 17 .
Phân tích phương án nhiễu.
Phương án A: Sai do HS giải đúng được a = - 1 , b = 4 nhưng lại tính sai a 2 + b 2 = 15 hoặc do HS giải sai bất phương trình. Cụ thể:
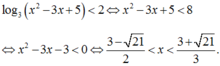
Suy ra a = 3 - 5 2 ; b = 3 + 5 2 Do đó tính được a 2 + b 2 = 15
Phương án B: Sai do HS giải sai bất phương trình. Cụ thể:
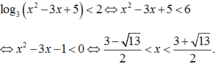
Suy ra a = 3 - 13 2 ; b = 3 + 13 2 Do đó tính được a 2 + b 2 = 11 .
MA
0
CM
13 tháng 1 2017
Điều kiện: -2 ≤ x≤ 4.
Xét 2 x 3 + 3 x 2 + 6 x + 16 - 4 - x trên đoạn [ -2; 4].
Có
f ' ( x ) = 3 ( x 2 + x + 1 ) 2 x 3 + 3 x 2 + 6 x + 16 + 1 2 4 - x > 0 ∀ x ∈ ( - 2 ; 4 ) .
Do đó hàm số đồng biến trên [-2; 4]
Bất phương trình đã cho trở thành f(x)≥ f(1) =2 3
Kết hợp với điều kiện hàm số đồng biến suy ra x≥1.
So với điều kiện, tập nghiệm của bpt là [1; 4].
Do đó; a2+ b2= 17.
Chọn D.
làm hộ
chị ơi em làm quen nha