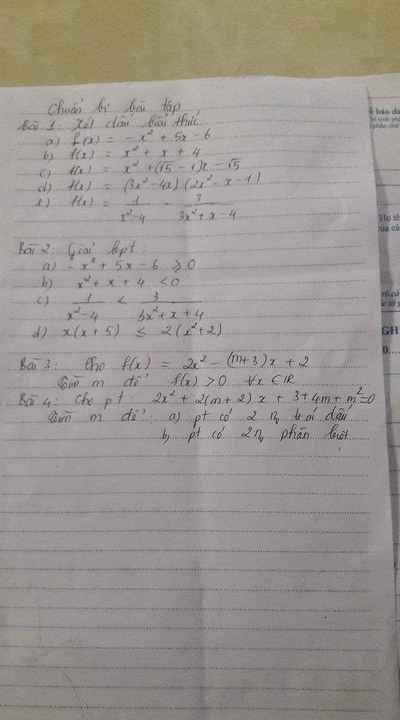Giải giúp mình từ bài 3 đến bài 6 ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 11 2021
Bài 6:
Vì \(m^2+1>0\) nên hs nghịch biến trong khoảng \(\left(-\infty;2m\right)\)
8 tháng 11 2021
Bài 3:
6: \(x< 0\) nên \(y=\sqrt[3]{x}\) nghịch biến
9 tháng 4 2021
a, 0 < a < \(\dfrac{\pi}{2}\) tức a là góc nhọn
⇒ sinA = \(\sqrt{1-\dfrac{16}{13^2}}=\dfrac{3\sqrt{17}}{13}\)
tan = sin/cos
cot = cos/sin (cái này tự tính nhá)
b, \(\dfrac{3\pi}{2}< a< 2\pi\) ⇔ \(270^0< a< 360^0\)
⇒ sin(a) < 0
cos (a) > 0
cot = - 3 => tan = \(\dfrac{-1}{3}\)
\(\dfrac{sin}{cos}=\dfrac{-1}{3}\), mà sin^2 + cos^2 = 1
sin < 0; cos >0
⇒ \(\left\{{}\begin{matrix}sin=-\dfrac{\sqrt{10}}{10}\\cos=\dfrac{3\sqrt{10}}{10}\end{matrix}\right.\)
PK
5
TA
18 tháng 5 2021
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
\(\dfrac{tanx-tany}{coty-cotx}=\dfrac{tanx-tany}{\dfrac{1}{tany}-\dfrac{1}{tanx}}=\dfrac{tanx-tany}{\left(\dfrac{tanx-tany}{tanx.tany}\right)}=\dfrac{tanx.tany\left(tanx-tany\right)}{tanx-tany}=tanx.tany\)
5 tháng 2 2021
Bài 20
Hệ (1) ⇔ \(\left\{{}\begin{matrix}1< x< 4\\x\le m-1\end{matrix}\right.\)
Đặt hai tập hợp A = (1 ; 4) và B = (\(-\infty\); m - 1]
Nếu m - 1 ≤ 1 tức m ≤ 2 thì A \(\cap\) B = ∅, hệ vô nghiệm
Nếu 1 < m - 1 < 4 tức 2 < m < 5 thì
A \(\cap\) B = (1; m - 1), tập nghiệm của hệ là (1; m - 1)
Nếu m - 1 ≥ 4 tức m ≥ 5 thì A \(\subset\) B. Tập nghiệm của hệ là A = (1; 4)
