K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
14.
A là khẳng định sai, CD không vuông góc SB
(Vì nếu \(CD\perp SB\) (1); do \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SAB\right)\Rightarrow CD\perp AB\) (vô lý do \(CD||AB\))
AH
Akai Haruma
Giáo viên
9 tháng 8 2021
Câu 84:
$\sin 3x+2\cos ^2x=1$
$\sin 3x=1-2\cos ^2x=-\cos 2x=\sin (2x-\frac{\pi}{2})$
\(\Rightarrow \left[\begin{matrix} 3x=2x-\frac{\pi}{2}+2k\pi\\ 3x=\frac{3}{2}\pi-2x+2k\pi\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=(2k+\frac{3}{2})\pi\\ x=\frac{2k+\frac{3}{2}}{5}\pi\end{matrix}\right.\) với $k$ nguyên
Nghiệm âm lớn nhất của pt:
$x=\frac{2(-1)+\frac{3}{2}}{5}\pi =\frac{-\pi}{10}$
HP
9 tháng 8 2021
84.
\(sin3x+2cos^2x=1\)
\(\Leftrightarrow sin3x+cos2x=0\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-3x\right)+cos2x=0\)
\(\Leftrightarrow2cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right).cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right)=0\\cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{4}-\dfrac{x}{2}=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{4}-\dfrac{5x}{2}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}-k2\pi\\x=-\dfrac{\pi}{10}-\dfrac{k2\pi}{5}\end{matrix}\right.\)
\(x=-\dfrac{\pi}{2}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{4}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{2}\)
\(x=-\dfrac{\pi}{10}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{20}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{10}\)
Vậy \(x=-\dfrac{\pi}{10}\) là nghiệm âm lớn nhất
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
ĐKXĐ: \(1-3m\ge0\Rightarrow m\le\dfrac{1}{3}\) (1)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(m^2+\left(1-3m\right)\ge\left(m-2\right)^2\)
\(\Leftrightarrow1-3m\ge-4m+4\Rightarrow m\ge3\) (2)
Kết hợp (1); (2) \(\Rightarrow\) không tồn tại m thỏa mãn
25 tháng 8 2021
Câu 19 : Phép đối xứng qua tâm M biến đường tròn (O;R) thành đường tròn (O' ; R)
=> Đường tròn này cố định
H thuộc đường tròn này đấy. CM thì dùng Kiến thức lớp 9 ấy. Thế nhá
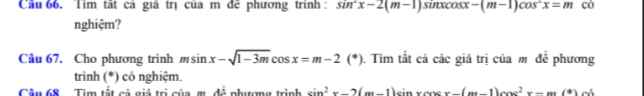
13.
Có \(3!\) cách sắp xếp 3 người phái đoàn Anh ngồi cạnh nhau.
Có \(5!\) cách sắp xếp 5 người phái đoàn Pháp ngồi cạnh nhau.
Có \(7!\) cách sắp xếp 7 người phái đoàn Mỹ ngồi cạnh nhau.
Có \(2!\) cách sắp xếp 3 phái đoàn vào bàn tròn.
\(\Rightarrow\) Có \(\Rightarrow3!.5!.7!.2!=7257600\) cách sắp xếp thỏa mãn yêu cầu bào toán.
14.
Có \(21!\) cách sắp xếp 21 bạn nam thành một dãy.
Có \(20!\) cách sắp xếp 20 bạn nữ xen kẽ giữa các bạn nam.
\(\Rightarrow\) Có \(20!.21!\) cách sắp xếp thỏa mãn yêu cầu bài toán.