K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KL
3
KL
6 tháng 9 2021
\(\orbr{\frac{1}{1-\sqrt{x}}-\frac{1}{\sqrt{x}}]}\div\orbr{\begin{cases}\\\end{cases}(2\sqrt{x}-1)(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x})]}\)
sori mng em bị lag xíu
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 1:
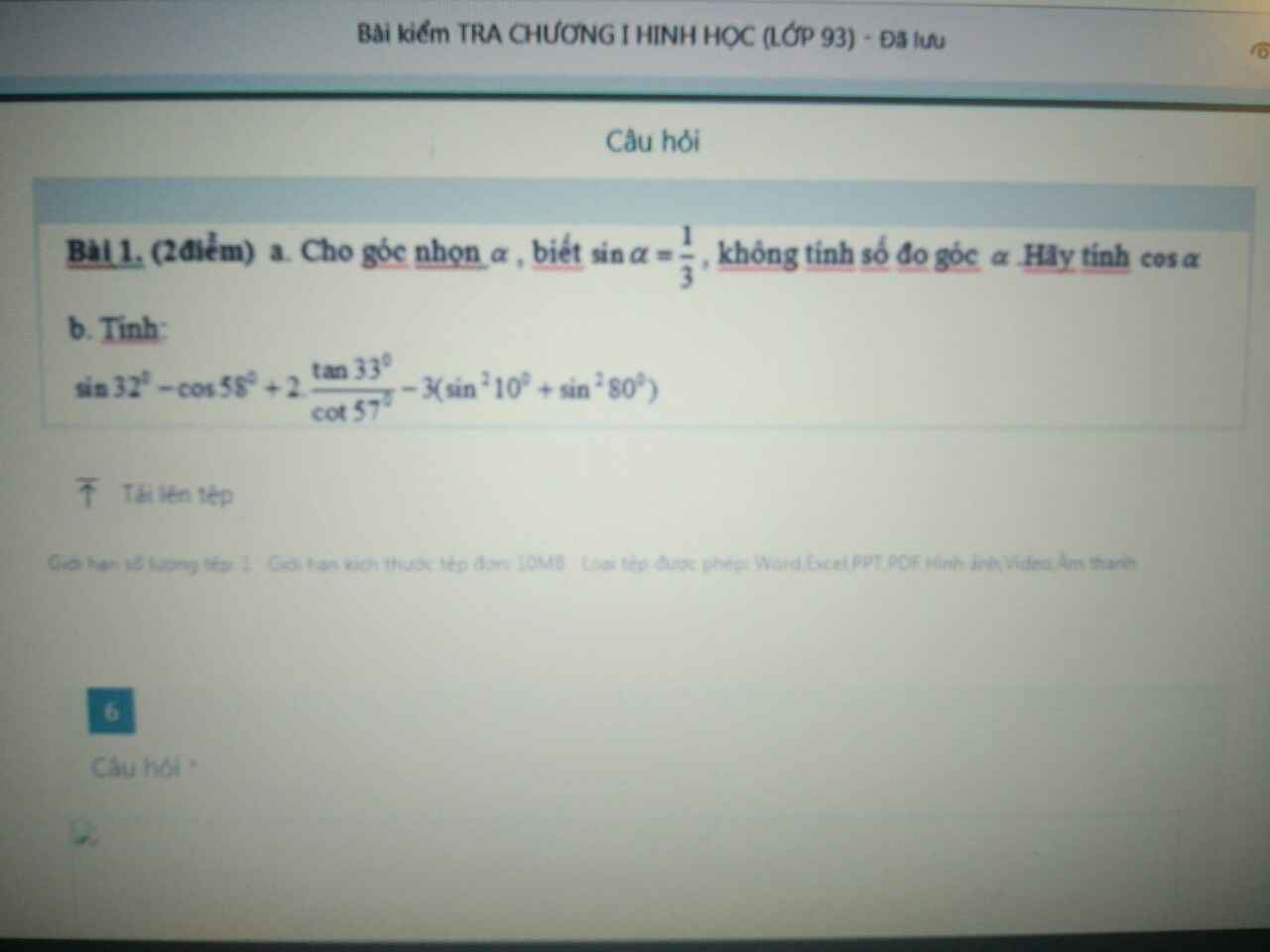
a. $\sin ^2a+\cos ^2a=1$
$\cos ^2a=1-\sin ^2a=1-(\frac{1}{3})^2=\frac{8}{9}$
$\Rightarrow \cos a=\frac{2\sqrt{2}}{3}$ (do $\cos a>0$)
b.
\(\sin 32-\cos 58+2\frac{\tan 33}{\cot 57}-3(\sin ^210+\sin ^280)\)
\(=\cos (90-32)-\cos 58+2\frac{\tan 33}{\tan (90-57)}-3(\sin ^210+\cos ^2(90-80))\)
\(=\cos 58-\cos 58+2\frac{\tan 33}{\tan 33}-3(\sin ^210+\cos ^210)\)
\(=0+2.1-3.1=-1\)
LD
2
22 tháng 10 2021
\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
22 tháng 10 2021
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)
TN
2
25 tháng 10 2021
\(\left(\sqrt{7}+\sqrt{6}\right)^2+\sqrt{168}\)
\(=7+6+2\sqrt{42}+2\sqrt{42}=13+4\sqrt{42}\)
HN
3
12 tháng 9 2021
đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
ĐKXĐ: \(x\ge0;x\ne4\)
\(A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
M
0
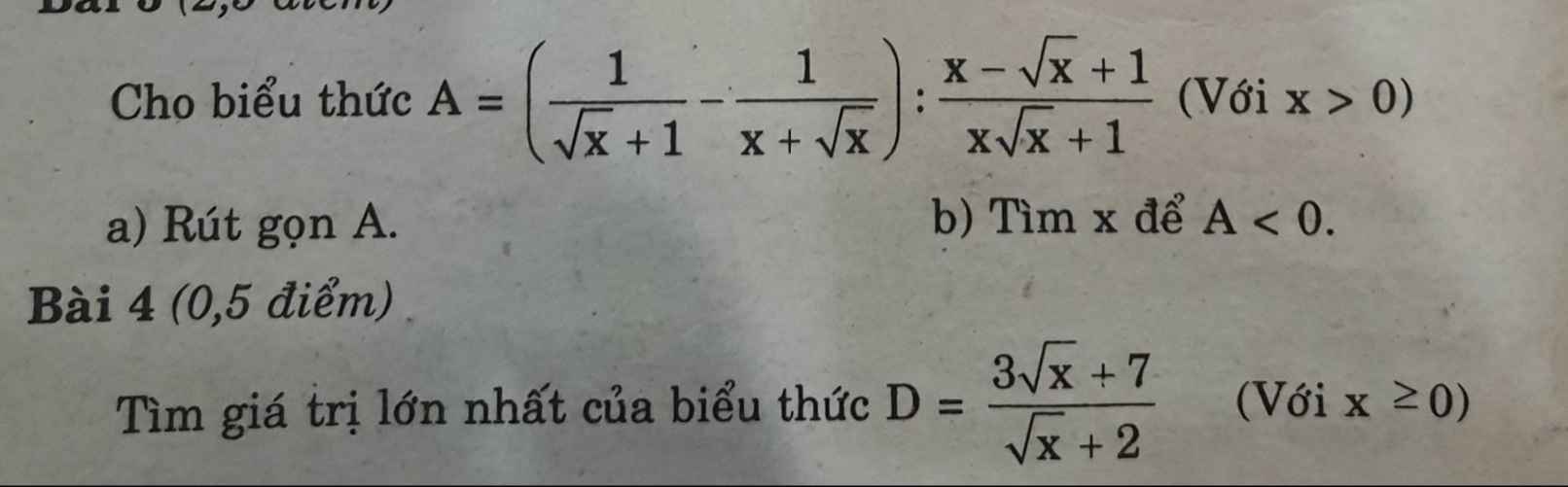
a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{x+\sqrt{x}}\right):\dfrac{x-\sqrt{x}+1}{x\sqrt{x}+1}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{x-1}{\sqrt{x}}\)
b: Để A<0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: 0<x<1
với \(x\ge0\) ta có :\(D=\dfrac{3\sqrt{x+7}}{\sqrt{x}+2}=\dfrac{3\left(\sqrt{x}+2\right)+1}{\sqrt{x}+2}=3+\dfrac{1}{\sqrt{x}+2}\)
D lớn nhất \(\Leftrightarrow\sqrt{x}+2\) nhỏ nhất:
Mà:\(\sqrt{x}+2\ge2\)
vậy:\(\max\limits_D=3+\dfrac{1}{2}=\dfrac{7}{2}\Leftrightarrow x=0\)