Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
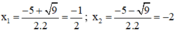
Vậy phương trình có tập nghiệm 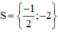
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
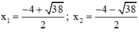
Vậy phương trình có tập nghiệm 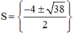
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
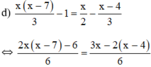
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
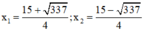
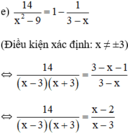
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
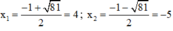
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
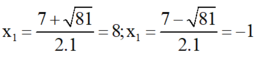
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8

Bài 5:
a. 1 - 2y + y2
= (1 - y)2
b. (x + 1)2 - 25
= (x + 1)2 - 52
= (x + 1 - 5)(x + 1 + 5)
= (x - 4)(x + 6)
c. 1 - 4x2
= 12 - (2x)2
= (1 - 2x)(1 + 2x)
d. 8 - 27x3
= 23 - (3x)3
= (2 - 3x)(4 + 6x + 9x2)
e. (đề hơi khó hiểu ''x3'' !?)
g. x3 + 8y3
= (x + 2y)(x2 - 2xy + y2)

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
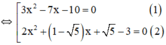
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
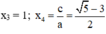
Vậy phương trình có tập nghiệm 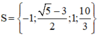
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
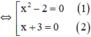
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
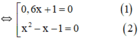
+ Giải (1): 0,6x + 1 = 0 ⇔ 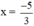
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 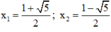
Vậy phương trình có tập nghiệm 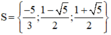
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
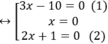
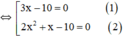
+ Giải (1): 3x – 10 = 0 ⇔ 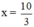
+ Giải (2):
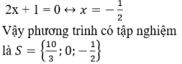


2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1

a)
5 x 2 − 3 x + 1 = 2 x + 11 ⇔ 5 x 2 − 3 x + 1 − 2 x − 11 = 0 ⇔ 5 x 2 − 5 x − 10 = 0
Có a = 5; b = -5; c = -10 ⇒ a - b + c = 0
⇒ Phương trình có hai nghiệm: x 1 = - 1 v à x 2 = - c / a = 2 .
Vậy phương trình có tập nghiệm S = {-1; 2}.
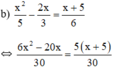
⇔ 6 x 2 − 20 x = 5 ( x + 5 ) ⇔ 6 x 2 − 20 x − 5 x − 25 = 0 ⇔ 6 x 2 − 25 x − 25 = 0
Có a = 6; b = -25; c = -25
⇒ Δ = ( - 25 ) 2 – 4 . 6 . ( - 25 ) = 1225 > 0
⇒ Phương trình có hai nghiệm
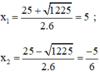
Vậy phương trình có tập nghiệm 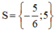
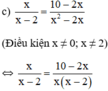
⇔ x 2 = 10 − 2 x ⇔ x 2 + 2 x − 10 = 0
Có a = 1; b = 2; c = -10 ⇒ Δ ’ = 1 2 – 1 . ( - 10 ) = 11 > 0
⇒ Phương trình có hai nghiệm
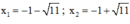
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm 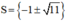
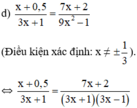
⇔ ( x + 0 , 5 ) ⋅ ( 3 x − 1 ) = 7 x + 2 ⇔ 3 x 2 + 1 , 5 x − x − 0 , 5 = 7 x + 2 ⇔ 3 x 2 − 6 , 5 x − 2 , 5 = 0
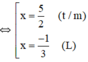
Vậy phương trình có tập nghiệm 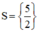
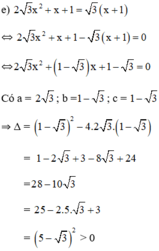
⇒ Phương trình có hai nghiệm
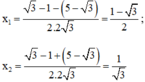
Vậy phương trình có tập nghiệm 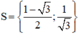
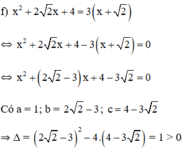
Phương trình có hai nghiệm:
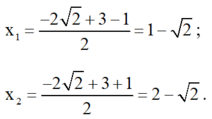
Vậy phương trình có tập nghiệm ![]()
\(4,\sqrt{x}+2=x+2,\)
\(\Rightarrow\sqrt{x}+2-x-2=0\)
\(\Rightarrow x-\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x}-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\\sqrt{x}=1\end{cases}}}\)
\(\Rightarrow x\in\left\{0;1\right\}\)