Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi m=0 thì (1) sẽ là x^2-5x+6=0
=>x=2 hoặc x=3
b: 2x1+3x2=13 và x1+x2=m+5
=>2x1+2x2=2m+10 và 2x1+3x2=13
=>x2=13-2m-10=3-2m và x1=m+5-3+2m=3m+2
x1x2=-m+6
=>(-2m+3)(3m+2)=-m+6
=>-6m^2-4m+9m+6=-m+6
=>-6m^2+6m=0
=>m=0 hoặc m=1

\(\Leftrightarrow\left(x^2-2x\right)^2+x^2-2x+1-13=0\)
\(\Leftrightarrow\left(x^2-2x\right)^2+x^2-2x-12=0\)
Đặt \(x^2-2x=t\Rightarrow t^2+t-12=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x=3\\x^2-2x=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-3=0\\x^2-2x+4=0\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)

bạn đăng tách ra cho mn giúp nhé
a, Để pt có 2 nghiệm pb
\(\Delta'=1-m\ge0\Leftrightarrow m\le1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\left(1\right)\\x_1x_2=m\left(2\right)\end{matrix}\right.\)
\(x_1-3x_2=0\)(3)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_1=-2\\x_2=-2-x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Thay vào (2) ta được \(m=\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)=\dfrac{3}{4}\)
\(b,\Delta=\left(m+5\right)^2-4\left(-m+6\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-7-4\sqrt{3}\\m\ge-7+4\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x1+x2=m+5\\2x1+3x2=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x1+2x2=2m+10\\2x1+3x2=13\end{matrix}\right.\)\(\)
\(\Rightarrow x2=13-2m-10=3-2m\Rightarrow x1=m+5-x2=m+5-3+2m=3m+2\)
\(x1x2=6-m\Rightarrow\left(3-2m\right)\left(3m+2\right)=6-m\Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=1\left(tm\right)\end{matrix}\right.\)
\(c,\Delta'=\left(m+1\right)^2-\left(m^2-2m+29\right)\ge0\Leftrightarrow m\ge7\)
\(\Rightarrow\left\{{}\begin{matrix}x1+x2=2m+2\\x1=2x2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x2=\dfrac{2m+2}{3}\\x1=\dfrac{2\left(2m+2\right)}{3}\end{matrix}\right.\)
\(\Rightarrow x1.x2=\dfrac{\left(2m+2\right).2\left(2m+2\right)}{9}=m^2-2m+29\Leftrightarrow\left[{}\begin{matrix}m=11\left(tm\right)\\m=23\left(tm\right)\end{matrix}\right.\)

a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
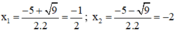
Vậy phương trình có tập nghiệm 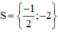
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
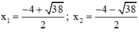
Vậy phương trình có tập nghiệm 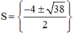
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
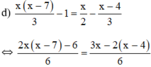
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
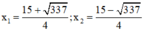
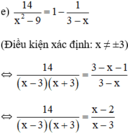
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
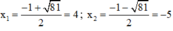
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
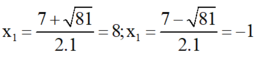
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8

a ) x 2 – 5 = 0 ⇔ x 2 = 5 ⇔ x 1 = √ 5 ; x 2 = - √ 5
Vậy phương trình có hai nghiệm x 1 = √ 5 ; x 2 = - √ 5
Cách khác:
x 2 – 5 = 0 ⇔ x 2 – ( √ 5 ) 2 = 0
⇔ (x - √5)(x + √5) = 0
hoặc x - √5 = 0 ⇔ x = √5
hoặc x + √5 = 0 ⇔ x = -√5
b)
x 2 – 2 √ 11 x + 11 = 0 ⇔ x 2 – 2 √ 11 x + ( √ 11 ) 2 = 0 ⇔ ( x - √ 11 ) 2 = 0
⇔ x - √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11

Phương trình x + x − 1 = 0 có chứa căn thức bên không là phương trình bậc hai một ẩn.
Phương trình 2x + 2y2 + 3 = 9 có chứa hai biến x; y nên không là phương trình bậc hai một ẩn.
Phương trình 1 x 2 + x + 1 = 0 có chứa ẩn ở mẫu thức nên không là phương trình bậc hai một ẩn.
Phương trình 2 x2 + 1 = 0 và x2 + 2019x = 0 là những phương trình bậc hai một ẩn.
Vậy có hai phương trình bậc hai một ẩn trong số các phương trình đã cho.
Đáp án cần chọn là: A

b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
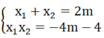
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
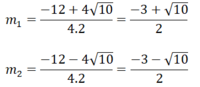
Vậy với 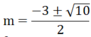 thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
a. Ta có: x2-11=0
⇌ x2=11
⇌\(\left[{}\begin{matrix}x=\sqrt{11}\\x=-\sqrt{11}\end{matrix}\right.\)
b.Ta có: x2-2\(\sqrt{13}\)x+\(\sqrt{13}\)=0
⇌(x-\(\sqrt{13}\))2=0
⇌ x-\(\sqrt{13}\)=0
⇌ x=\(\sqrt{13}\)
c. Ta có : x2-9x+14=0
⇌ (x-7)(x-2)=0
⇌\(\left[{}\begin{matrix}x-7=0\\z-2=0\end{matrix}\right.\)⇌\(\left[{}\begin{matrix}x=7\\x=2\end{matrix}\right.\)
d.Ta có \(\sqrt{x}\)-6=13
⇌\(\sqrt{x}\)=19
⇌x = 361
e.Ta có: \(\sqrt{x}\)+9=3
Vì \(\sqrt{x}\)≥0∀x⇒\(\sqrt{x}\)+9≥9
⇒ ptvn
f.Ta có:\(\sqrt{x^2}\)-2x+4=x-1
⇌ |x|-3x-5=0(*)
TH1: x≥0
⇒ pt(*) ⇌ x-3x+5=0⇌-2x-5=0⇒x=\(\dfrac{5}{2}\)(t/m)
TH2: x<0
⇒ pt(*) ⇌ -x-3x+5=0⇌-4x+5=0⇒x=\(\dfrac{5}{4}\)(l)
Vậy x=\(\dfrac{5}{2}\)là nghiệm của phương trình