PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
30 tháng 3 2016
Ta có điều kiện của bất phương trình là
\(x^2+2x-8>0\)
Khi đó ta có thể viết bất phương trình dưới dạng :
\(\log_{\frac{1}{2}}\left(x^2+2x-8\right)\ge\log_{\frac{1}{2}}16\)
Vì cơ số \(\frac{1}{2}\) nhỏ hơn 1 nên bất phương trình trên tương đương với hệ
\(\begin{cases}x^2+2x-8>0\\x^2+2x-8\le16\end{cases}\) \(\Leftrightarrow\begin{cases}x<-4Vx>2\\-6\le x\le4\end{cases}\)\(-6\le\)x\(\le-4\) và 2<x\(\le4\)
Vậy tập nghiệm của bất phương trình đã cho là
\(D=\left(-6;4\right)\cup\left(2;4\right)\)
PT
1
CM
30 tháng 11 2019
ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
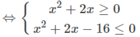
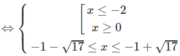
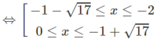
Vậy tập nghiệm là
PT
1
CM
1 tháng 3 2018
Bất phương trình đã cho tương đương với hệ:
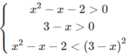
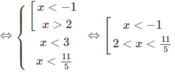
Vậy tập nghiệm là (− ∞ ; −1) ∪ (2; 11/5)
PT
1
CM
3 tháng 9 2019
2 x - 2 > 2 2 x + 1
⇔ |x−2| > 2|x+1|
⇔ x 2 − 4x + 4 > 4( x 2 + 2x + 1)
⇔ 3 x 2 + 12x < 0
⇔ −4 < x < 0
CM
11 tháng 3 2018
a) Bất phương trình đã cho tương đương với hệ sau:
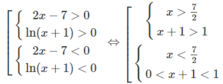
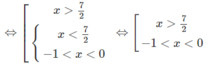
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
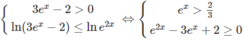
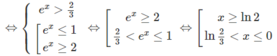
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
2 2 x - 2 . 2 x + 8 < 2 3 x . 2 1 - x ⇔ 2 2 x + 2 . 2 x - 8 > 0