Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ bài toán, ta có hình ảnh:
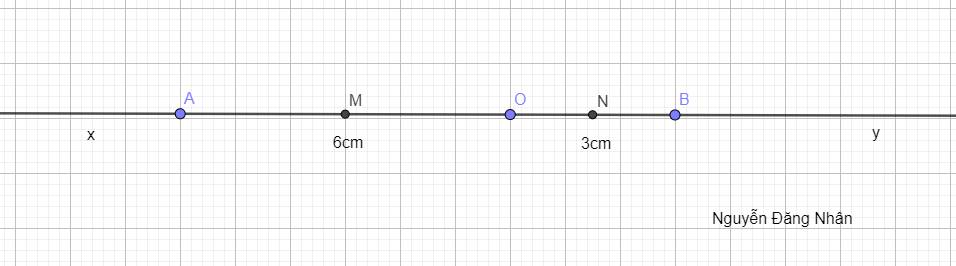
A) Vì M nằm ở tia Ox (bên trái O), N nằm ở tia Oy (bên phải O) nên điểm nằm giữa 2 điểm còn lại là điểm O (nằm giữa M và N)
B) Vì M là trung điểm OA, ta có:
\(OM=\dfrac{OA}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Tương tự, N là trung điểm của OB, ta có:
\(ON=\dfrac{OB}{2}=\dfrac{3}{2}=1,5\left(cm\right)\)
Vì O nằm giữa MN (ở phần A), nên ta có:
\(MN=OM+ON=3+1,5=4,5\left(cm\right)\)

a, Ta có : OA + AB = OB => AB = OB - OA = 5 - 3 = 2 cm
b, Ta có : OC + OA = AC => OC = AC - OA = 6 - 3 = 3 cm
Vậy OA = OC ( 3cm = 3cm )

a) Chỉ ra điểm O nằm giữa hai điểm B và A. Từ đó tính được AB = 5 cm.
b) Chỉ ra điểm B nằm giữa hai điểm A và C. Từ đó tính được AC = 10 cm.

a: Trên tia Ox, ta có: OA<OB
nên điểm A nằm giữa hai điểm O và B
b: Trên tia Ox, ta có: OA<OC
nên điểm A nằm giữa hai điểm O và C
=>OA+AC=OC
hay AC=3(cm)
Ta có: A nằm giữa O và C
mà AO=AC
nên A là trung điểm của OC

a. Để xác định điểm nào nằm giữa hai điểm còn lại, ta cần so sánh độ dài các cạnh. Ta có:
OA = 3 cm < OC = 6 cm, nên A nằm giữa O và C.
OB = 8 cm > OC = 6 cm, nên B không nằm giữa O và C. Vậy điểm A nằm giữa B và C.
b. Để xác định xem điểm A có phải trung tâm của đoạn thẳng OC hay không, ta cần tính độ dài các cạnh. Ta có: OA = 3 cm, OC = 6 cm. Nếu A là trung tâm của OC, thì ta có: OA = AC = OC/2 = 6/2 = 3 cm. Vậy ta thấy A không phải trung tâm của OC vì OA ≠ AC.
c. Để so sánh độ dài đoạn thẳng AD và OB, ta cần tính độ dài các cạnh. Ta có: OD = 6 cm, OA = 3 cm, OB = 8 cm. Áp dụng định lí Pytago:
Tam giác OAD vuông tại A, có cạnh huyền là OD, nên: AD² = OA² + OD² = 3² + 6² = 45 cm²
Tam giác OAB vuông tại A, có cạnh huyền là OB, nên: AB² = OA² + OB² = 3² + 8² = 73 cm². Do đó, ta có: AD² < AB² => AD < AB. Vậy độ dài đoạn thẳng AD nhỏ hơn độ dài đoạn thẳng OB.

Vì điểm O thuộc đường thẳng xy => Hai tia Ox, Oy đối nhau
Vì điểm A thuộc tia Ox
điểm B thuộc tia đối của tia Ox => Điểm O nằm giữa 2 điểm A và B => OA + OB = AB . Thay số :
3 + 9 = AB => AB = 12 cm
Có : \(\hept{\begin{cases}OC=1cm\\OB=9cm\end{cases}}\Rightarrow OC< OB\)
Trên cùng 1 tia Oy có OC < OB => Điểm C nằm giữa 2 điểm O và B => OC + BC = OB . thay số :
1 + BC = 9 => BC = 9 - 1 = 8 ( cm )
b) Vì điểm M là trung điểm của BC = 8cm => \(CM=CB=\frac{BC}{2}=\frac{8}{2}=4\left(cm\right)\)
Vì điểm M là trung điểm của BC => Điểm M nằm giữa B;C (1)
Mà điểm C nằm giữa hai điểm O và B (2)
Từ (1); (2) => Điểm C nằm giữa O và M => OC + CM = OM . Thay số :
1 + 4 = OM => OM = 5 ( cm )
a,Vì O nằm trên đường thẳng xy
=> 2 tia Ox, Oy đối nhau
Mà điểm A nằm trên tia Ox, điểm B nằm trên tia Oy
=> OA, OB đối nhau => O nằm giữa A và B
=> OA + OB = AB
=> AB = 3 + 9 = 12 (cm)
Vì 2 điểm C,B nằm cùng phía trên tia Oy mà OC < OB ( 1cm < 9cm )
=> C nằm giữa O và B
=> OC + BC = OB
=> BC = OB - OC = 9 - 1 = 8 (cm)
Vậy AB = 12 cm
BC = 8 cm
b, Vì M là trung điểm của BC
=> CM = BM = BC/2 = 8/2 = 4 (cm)
Vì điểm M nằm giữa B và C , điểm C nằm giữa O và M
=> C nằm giữa O và M
=> OM = OC + CM = 1 + 4 = 5 (cm)
Vậy CM= 4cm
OM = 5 cm

a. So sánh OA và OB rồi cho biết điểm nào nằm giữa hai điểm còn lại?
Trên tia Ox, ta có: OA < OB (vì 3cm < 5cm)
=> Điểm A nằm giữa O và B
b. Tính AB?
Ta có: Điểm A nằm giữa O và B
=> OA + AB = OB
Hay 3 + AB = 5
=> AB = 5 - 3 = 2(cm)
c. Tính AC?
Ta có: Điểm O nằm giữa A và C
=> AO + OC = AC
Hay 3 + 4 + AC
=> AC = 7(cm)
a: AB=OA+OB=m+5
b: Vì OB<OC
nên B nằm giữa O và C
c: B là trung điểm của OC
=>OB=BC
=>m=6/2=3cm