Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
 Em có bài này muốn hỏi mọi người ạ, em đã cô lập được logy(x) nhưng tìm max min 2 ẩn vẫn khó quá :(.
Em có bài này muốn hỏi mọi người ạ, em đã cô lập được logy(x) nhưng tìm max min 2 ẩn vẫn khó quá :(.

Đề bài liệu có chính xác không nhỉ? Mình chỉ có thể tìm được max bằng \(2\sqrt{2}\) (xảy ra khi \(lnx=\sqrt{2}\) và \(lny=\dfrac{1}{2}\)) và ko thể tìm được min.
À rồi OK, suy nghĩ hơi cồng kềnh 1 xíu nên hướng tìm min bị sai:
Giả thiết tương đương: \(y^{\sqrt{4-ln^2x}}=x^{1-lny}\)
\(\Rightarrow\sqrt{4-ln^2x}.lny=\left(1-lny\right)lnx\) (1)
Do \(y\ne1\Rightarrow lny\ne0\)
Nên (1) tương đương: \(\sqrt{4-ln^2x}=\left(\dfrac{1-lny}{lny}\right)lnx\) (2)
Đặt \(\left\{{}\begin{matrix}lnx=a\\lny=b\end{matrix}\right.\) thì \(log_yx=\dfrac{a}{b}\)
(2) trở thành: \(\sqrt{4-a^2}=\left(\dfrac{1-b}{b}\right)a\)
\(\Rightarrow\sqrt{4-a^2}=\dfrac{a}{b}-a\Rightarrow\dfrac{a}{b}=\sqrt{4-a^2}+a\)
Xét hàm \(f\left(a\right)=\sqrt{4-a^2}+a\) trên \(\left[-2;2\right]\)
\(f'\left(a\right)=1-\dfrac{a}{\sqrt{4-a^2}}=0\Rightarrow a=\sqrt{2}\)
\(f\left(-2\right)=-2\) ; \(f\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(a\right)_{min}=-2\) ; \(f\left(a\right)_{max}=2\sqrt{2}\)
Đáp án B

Hệ số bất định:
\(\dfrac{x^2-3}{x\left(x^2+1\right)\left(x^2+2\right)}=\dfrac{a}{x}+\dfrac{bx}{x^2+1}+\dfrac{cx}{x^2+2}\)

Lời giải:
\(\lim\limits_{x\to 2-}y=\lim\limits_{x\to 2-}\frac{\sqrt{4-x^2}}{(x-2)(x-3)}=\lim\limits_{x\to 2-}\frac{\sqrt{2+x}}{\sqrt{2-x}(x-3)}=-\infty \) nên $x=2$ là TCĐ
Vì \(x\in [-2;2)\) nên không tồn tại \(\lim\limits_{x\to +\infty }y\) nên đths không có TCN
Còn $x=3$ không thể là TCĐ vì tại $x=3$ thì $\sqrt{4-x^2}$ không tồn tại .

3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
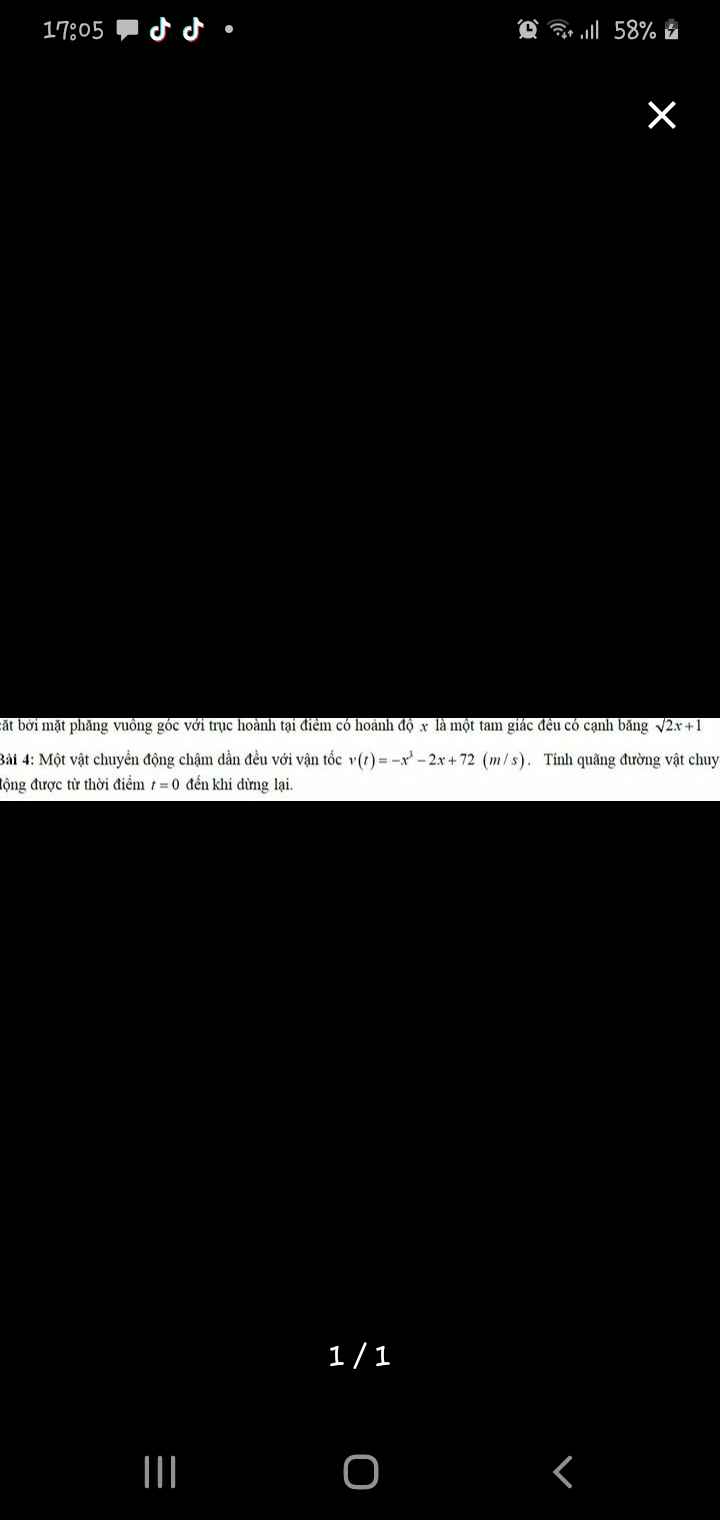 Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢





Việc gọi ẩn ko ảnh hưởng gì tới kết quả bài toán cả, cứ thoải mái đi