Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ ẹt;
Giả sử \(\Delta\)ABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên \(\left(\frac{BI}{AC}\right)=\left(\frac{BD}{DC}\right)=\left(\frac{BD}{3BD}\right)=\frac{1}{3}\) (định lí Ta lét)
mà BI=AB nên \(\frac{AB}{AC}=\frac{1}{3}\)
Cm \(\Delta\)AHC đồng dạng \(\Delta\)BHA(g.g) nên \(\frac{BH}{HA}=\frac{HA}{HC}=\frac{AB}{AC}=\frac{1}{3}\)
nên \(BH=\frac{1}{3}AH\);\(HC=3AH\)nên \(\frac{BH}{HC}=\frac{1}{9}\)

Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)

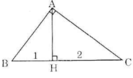
ΔABC vuông tại A và đường cao AH như trên hình.
BC = BH + HC = 1 + 2 = 3
Theo định lí 1:
A B 2 = B H . B C = 1 . 3 = 3
=> AB = √3
Theo định lí 1:
A C 2 = H C . B C = 2 . 3 = 6
=> AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.

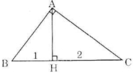
ΔABC vuông tại A và đường cao AH như trên hình.
BC = BH + HC = 1 + 2 = 3
Theo định lí 1: AB2 = BH.BC = 1.3 = 3
=> AB = √3
Theo định lí 1: AC2 = HC.BC = 2.3 = 6
=> AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.

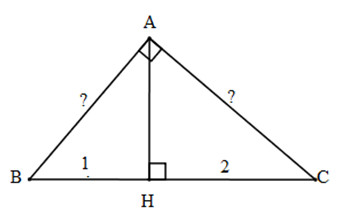
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH, ta có:
AH2=BH.CH⇒AH=√BH.CH=√1.2=√2
Áp dụng định lí Pytago vào tam giác ABH vuông tại H, ta có:
AH=√BH2+AH2=√1+2=√3AH=BH2+AH2=1+2=3
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
AC=√BC2−AB2=√32−3=√6AC=BC2−AB2=32−3=6

Giả sử tam giác ABC có góc BAC = 90o, AH ⊥ BC, BH = 3, CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC = 3.(3 + 4) = 3.7 = 21 ⇒ AB = \(\sqrt{21}\)
AC2 = CH.BC = 4.(3 + 4) = 4.7 = 28 ⇒ AC = \(\sqrt{28} = 2\sqrt{7} \)



Xét tam giác ABC vuông tại A với AB > AC, gọi AH là đường cao kẻ từ A thì ta có: