Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
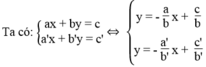
Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số góc và tung độ gốc bằng nhau:
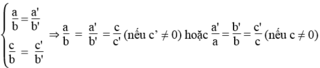
*a = 0, a’ ≠ 0
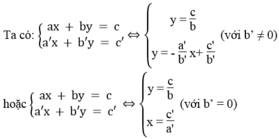
Vì hai đường thẳng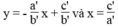 
luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
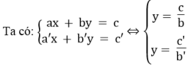
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
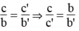
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
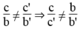
*b = 0, b’ ≠ 0
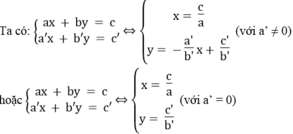
Vì hai đường thẳng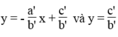 
luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
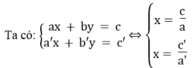
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
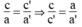
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
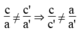
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
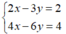
Vì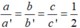 
nên hệ phương trình có vô số nghiệm
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
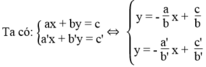
Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số góc bằng nhau và tung độ gốc khác nhau:
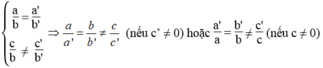
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
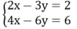
Vì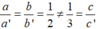 
nên hệ phương trình trên vô nghiệm
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.
Ta biết tập nghiệm của phương trình ax + by = c được biểu diễn bằng đường thẳng ax + by = c và tập nghiệm của phương trình a'x + b'y = c' được biểu diễn bằng đường thẳng a'x + b'y = c'.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
Vì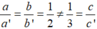
nên hệ phương trình trên vô nghiệm