K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
31 tháng 1 2018
t g 2 α - sin 2 α . t g 2 α = t g 2 α ( 1 - sin 2 α ) = t g 2 α sin 2 α + c o s 2 α - sin 2 α = t g 2 α . c o s 2 α = sin 2 α / c o s 2 α . c o s 2 α = sin 2 α
PT
1
CM
9 tháng 11 2019
cos 2 α + t g 2 α . cos 2 α = cos 2 α + sin 2 α / cos 2 α . cos 2 α = cos 2 α + sin 2 α = 1
CM
14 tháng 11 2019
1 – sin 2 α = ( sin 2 α + c o s 2 α ) – sin 2 α
= sin 2 α + c o s 2 α – sin 2 α = c o s 2 α
PT
1
CM
1 tháng 10 2018
b) tan 2 α - sin 2 α . tan 2 α
= tan 2 α (1 - sin 2 α )
= tan 2 α . cos 2 α
= sin 2 α
PT
1
CM
2 tháng 3 2019
sin 4 α + cos 4 α + 2 sin 2 α . cos 2 α = sin 2 α + cos 2 α 2 α = 1
PT
1
CM
28 tháng 6 2019
1 + sin 2 α + c o s 2 α = 1 + ( sin 2 α + c o s 2 α ) = 1 + 1 = 2
PT
1
CM
7 tháng 1 2017
b) sinα - sinα. c o s 2 α
= sinα (1 - c o s 2 α )
= sinα. sin 2 α
= sin 3 α
PT
1
CM
7 tháng 9 2019
c) sin 4 α + cos 4 α + 2 sin 2 α c o s 2 α
= sin 2 α + cos 2 α 2
= 1
PT
1
CM
24 tháng 4 2018
t g 2 α . 2 cos 2 α + sin 2 α - 1 = t g 2 α . cos 2 α + cos 2 α + sin 2 α - 1 = t g 2 α . cos 2 α + 1 - 1 = t g 2 α . cos 2 α = sin 2 α / cos 2 α . cos 2 α = sin 2 α
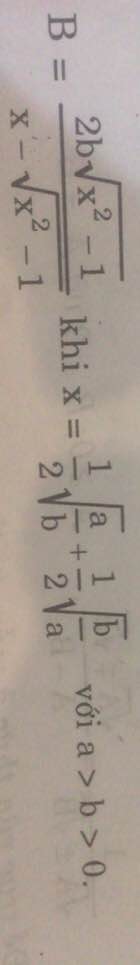
Lần sau đăng đề bạn nên gõ công thức cho gọn, đừng đăng ảnh dài oạch như thế này nhìn rất khó.
Lời giải:
Ta có:
\(x^2=\frac{1}{4}(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}})^2=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}+2)\)
\(\Rightarrow x^2-1=\frac{1}{4}(\frac{a}{b}+\frac{b}{a}-2)=\frac{1}{4}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})^2\)
\(\Rightarrow \sqrt{x^2-1}=\frac{1}{2}|\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}|=\frac{1}{2}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})\)
Do đó:
\(2b\sqrt{x^2-1}=b.\frac{a-b}{\sqrt{ab}}=(a-b).\sqrt{\frac{b}{a}}\)
\(x-\sqrt{x^2-1}=\frac{1}{2}[\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}-(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})]\)
\(=\sqrt{\frac{b}{a}}\)
$\Rightarrow B=a-b$