
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f\left(x-3\right)+5-m>0\)
\(\Leftrightarrow\left(x-3\right)^2+5-m>0\)
\(\Leftrightarrow x^2-6x+14-m>0\)
BPT có tập nghiệm là R khi:
\(\Delta'=9-\left(14-m\right)< 0\)
\(\Leftrightarrow m< 5\)

Để bất phương trình có tập nghiệm là R thì \(\left(m-2\right)^2-4\left(m+1\right)< 0\)
\(\Rightarrow m^2-4m+4-4m-4< 0\)
=>m(m-8)<0
=>0<m<8
Để bất phương trình đã cho có tập nghiệm là R thì
\(\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\) (với a là hệ số của x2 và bằng 1, thỏa)
\(\Rightarrow\) (m-2)2-4.(m+1)\(\le\)0 \(\Leftrightarrow\) m2-8m\(\le\)0 \(\Leftrightarrow\) 0\(\le\)m\(\le\)8.

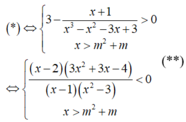
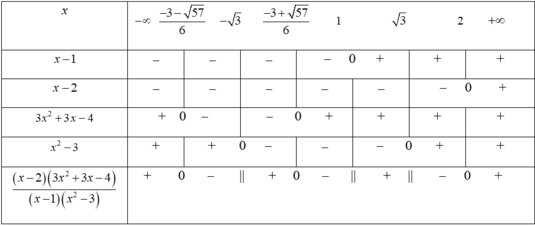
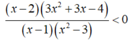 là
là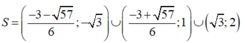
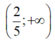
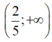
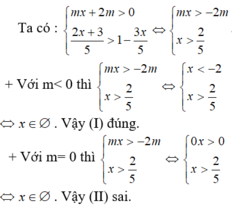
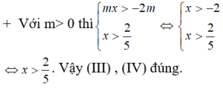
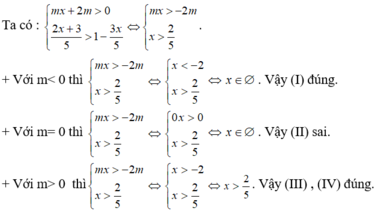
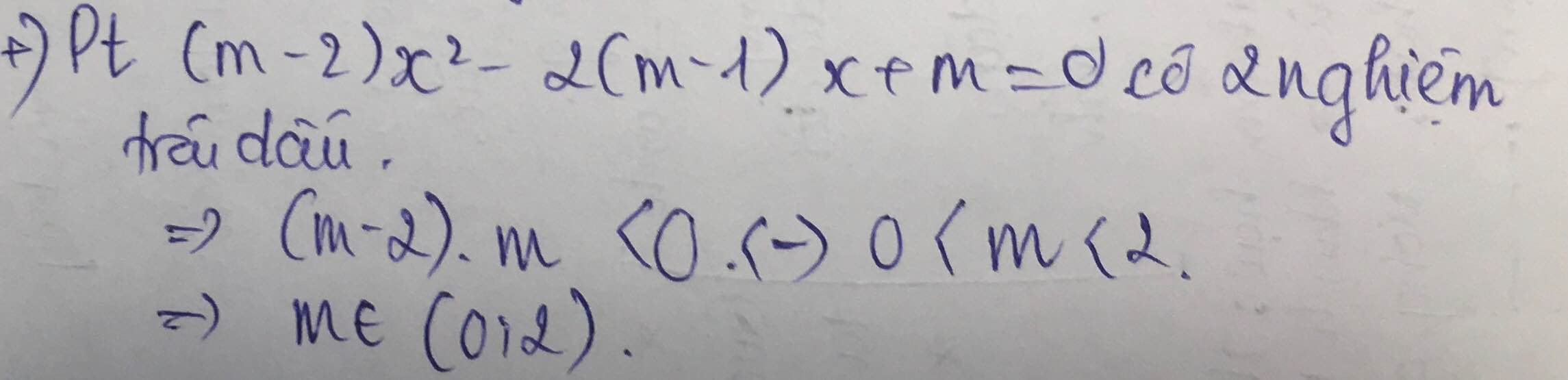

BPT có tập nghiệm là R khi và chỉ khi:
\(\Delta=\left(m+1\right)^2-4m^3\le0\)
\(\Leftrightarrow-4m^3+m^2+2m+1\le0\)
\(\Leftrightarrow\left(1-m\right)\left(4m^2+3m+1\right)\le0\) (1)
Do \(4m^2+3m+1=4\left(m+\dfrac{3}{8}\right)^2+\dfrac{7}{16}>0;\forall m\)
Nên (1) tương đương: \(1-m\le0\Rightarrow m\ge1\)