Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn lập tỉ số giữa H1 và H2
H1=1-R.P/U12
H2=1-R.P/U22
bạn chuyển vế rồi lập tỉ số vì R và P như nhau nên rút gọn
=>(1-H1)/(1-H2)=U22/U12
=>(1-0,84)/(1-0,96)=U22/102
=>U2=20kV
Chắc đúng hì
Hiệu suất từ 84% tăng lên 96% có nghĩa hao phí từ 16% giảm xuống 4% (giảm đi 4 lần)
Mà \(\Delta P =\dfrac{P^2.R}{U^2\cos^2\varphi}\)
Nên để \(\Delta P\) giảm 4 lần thì U tăng 2 lần, có giá trị là: \(10.2 = 20kV\)

Đáp án A
Cách giải:
Công suất nơi phát là: P
Công suất tiêu thụ của mỗi hộ dân là P0
+ Nếu tăng điện áp hiệu dụng nơi phát từ U lên 2U thì số hộ dân có đủ điện để tiêu thụ tăng từ 80 hộ lên 95 hộ
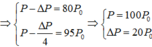
Sợi dây siêu dẫn có R = 0 => DP = 0 => P = 100P0 => số hộ dân đủ điện để tiêu thụ là 100 hộ

Chọn đáp án C
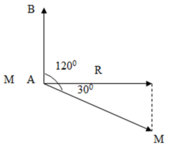
+ Công suất tiêu thụ không đổi nên: ![]()
+ Hệ số công suất của cuộn dây: ![]()

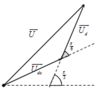
Biểu diễn vecto các điện áp.
Hiệu suất của động cơ H=A/P
→ P = A H = 8 , 5 0 , 85 = 10 kW.
→ Điện trở trong của động cơ R d c = P I 2 = 10000 50 2 = 4 Ω
→ Z d c = R cos 30 0 = 8 3 Ω.
→ U d c = I Z d c = 50 8 3 = 400 3 V.
Từ giản đồ vecto, ta thấy rằng góc hợp với U d c → và U d → là 150 độ .
→ U = 125 2 + 400 3 2 − 2.125. 400 3 cos 150 0 = 345 V
Đáp án B

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

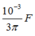
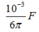
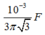
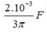
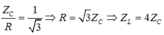
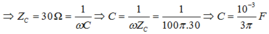
Công suất hao phí trong quá trình truyền đi là \(\Delta P = \frac{P^2}{U^2}R.(1)\)
=> \(H_1 = 1 - \frac{\Delta P_1}{P} =1 - \frac{P}{U_1^2}R.\)
\(H_2 = 1 - \frac{\Delta P_2}{P} =1 - \frac{P}{U_2^2}R.\)
Mà \(U_1 = 20kV; U_2 = 20+10 = 30kV.\)
=> \(\frac{1-H_1}{1-H_2} = \frac{U_2^2}{U_1^1} = \frac{9}{4}=> 4-4H_1 = 9-9H_2 \)
=> \(H_2 = \frac{5+4H_1}{9} = \frac{5+4.0,82}{9}=0,92 = 92\%.\)
Chọn đáp án.D