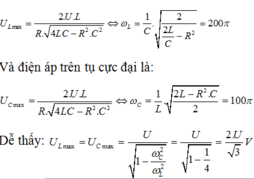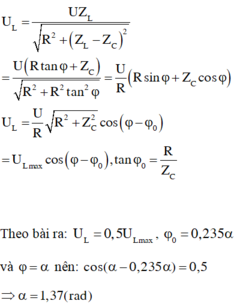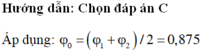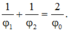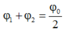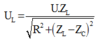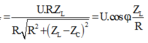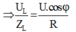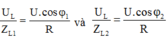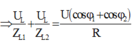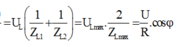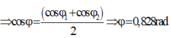Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

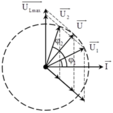
Ta biễu diễn trên giãn đồ vecto. Hai giá trị của L cho cùng một điện áp hiệu dụng trên cuộn cảm → U 1 → và U 2 → đối xứng với ứng với U L m a x
→ Ta có φ 1 + φ 2 = 2 φ 0 → φ 0 = 0 , 785 rad.
Đáp án C

Giải thích: Đáp án B
Khi C = C1, độ lệch pha của mạch: 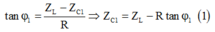
Khi C = C2, độ lệch pha của mạch: 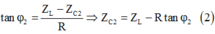
Từ (1) và (2) ta có: ![]()
Lấy (1). (2) ta có: ![]()
Khi C = C0, độ lệch pha của mạch:
Mà khi C = C1 và C = C2 điện áp hiệu dụng ở hai đầu tụ điện có cùng giá trị:
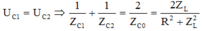
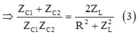
Từ (1), (2) và (3):
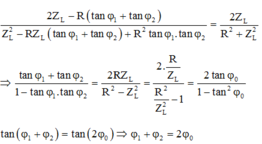

Đáp án B
Bổ đề : ![]()
Trong đó : + U L max là giá trị cực đại của U L khi L thay đổi.
+ φ 0 là độ lệch pha của u và i trong trường hợp U L max.
Áp dụng :
U
L
như nhau thì ![]()
Có 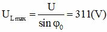
![]()

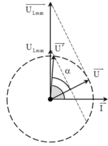
Biểu diễn vecto chung gốc I cho các điện áp.
→ Từ hình vẽ, ta có cosα = 0,5 → α=π/3.
Mặc khác φ = α + 0,25φ → φ = 1,4 rad.
Đáp án C

Mình giải thích rõ hơn công thức của bạn Nguyễn Trung Thành
Nhận xét:
+ Khi L thay đổi thì góc b và c không đổi (do R và ZC không đổi).
+ Khi L = L0 để UL max thì a0 + b = 900.
Áp dụng định lí hàm số sin trong tam giác OULUC:
\( \frac{U_L}{\sin(a+b)}=\frac{U}{\sin c}=const\)
\(\Rightarrow\frac{U_L}{\sin(a_1+b)}=\frac{U_L}{\sin(a_2+b)}\Rightarrow \sin(a_1+b)=\sin(a_2+b)\Rightarrow a_1+b=\pi-(a_2+b)\)
\(\Rightarrow a_1+a_2=\pi-2b\) Mà \(a_0+b=\frac{\pi}{2}\Rightarrow 2a_0=\pi-2b\)
\(\Rightarrow a_1+a_2=2a_0\)
Hay: \(\varphi_0=\frac{\varphi_1+\varphi_2}{2}\)
Áp dụng công thức: \(\varphi_0=\frac{\varphi_1+\varphi_2 }{2}\Rightarrow\varphi_0=\frac{0,56+0,98 }{2}=0,77\)
\(\Rightarrow \cos\varphi_0=\cos0,77=0,72\)
Đáp án B.

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
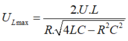
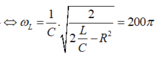
Và điện áp trên tụ cực đại là:
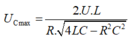
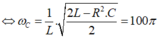
Dễ thấy:
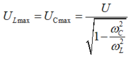
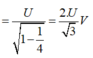

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có: