TC
8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 8 2021
\(\Leftrightarrow2cos^2x-1-\left(2m-3\right)cosx+m-1=0\)
\(\Leftrightarrow2cos^2x-\left(2m-3\right)cosx+m-2=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(cosx-m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=m-2\end{matrix}\right.\)
Do \(cosx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{3}+k2\pi\) ko có nghiệm thuộc khoảng đã chi
\(\Rightarrow cosx=m-2\) có nghiệm thuộc \(\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)
Ta có \(x\in\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\Rightarrow cosx\in\left(-1;0\right)\)
\(\Rightarrow-1< m-2< 0\)
\(\Rightarrow1< m< 2\)
DD
Đoàn Đức Hà
Giáo viên
29 tháng 3 2022
TH1: chọn \(1\)câu khó từ \(5\)câu: \(C^1_5\).
Chọn \(9\)câu trong đó có cả câu trung bình và câu dễ.
Ta sử dụng phần bù. Số cách là: \(C^9_{45}-C^9_{20}-C^9_{25}\).
TH cách số câu khó từ \(2\)đến \(5\)ta làm tương tự.
Khi đó có tổng số cách chọn \(10\)câu sao cho đủ 3 loại câu hỏi là:
\(C^1_5\left(C^9_{45}-C^9_{20}-C^9_{25}\right)+C^2_5\left(C^8_{45}-C^8_{20}-C^8_{25}\right)+C^3_5\left(C^7_{45}-C^7_{20}-C^7_{25}\right)\)
\(+C^4_5\left(C^6_{45}-C^6_{20}-C^6_{25}\right)+C^5_5\left(C^5_{45}-C^5_{20}-C^5_{25}\right)=7052230625\)
CM
19 tháng 9 2018
Số cách chọn ra 10 câu hỏi bất kỳ trong số 20 câu hỏi đã cho là 
.
+ Tiếp theo ta đếm số cách chọn ra 10 câu hỏi mà không có đủ cả ba loại câu hỏi ở trên:
Phương án 1: Trong 10 câu hỏi chọn ra chỉ bao gồm câu hỏi dễ và trung bình: 
cách.
Phương án 2: Trong 10 câu hỏi chọn ra chỉ bao gồm câu hỏi dễ và khó: 
cách.
Phương án 1: Trong 10 câu hỏi chọn ra chỉ bao gồm câu hỏi trung bình và khó: 
cách.
Từ đó suy ra số lượng đề thỏa mãn yêu cầu có thể lập được là:
Chọn A.
11 tháng 5 2016
http://www.toanhocnhatrang.com/2015/05/bai-toan-so-298.html
LT
11 tháng 5 2016
Gọi A là tập hợp cách chọn đề có 3 câu dễ, 1 câu khó, 1 câu trung bình.
B là tập hợp cách chọn đề có 2 câu dễ, 2 câu khó, 1 câu trung bình
C là tập hợp cách chọn đề có 2 câu dễ, 1 câu khó, 2 câu trung bình
D là tập hợp cách chọn đề thỏa mãn yêu cầu đề ra. Ta có:
D = A \(\cup\) B \(\cup\) C
ngoài ra A,B,C đôi một không giao nhau. Theo quy tắc cộng ta có
\(\left|D\right|\) = \(\left|A\right|\) + \(\left|B\right|\) + \(\left|C\right|\) (1)
Theo quy tắc nhân ta có
\(\left|A\right|\) = \(C_{15}^3\).\(C_5^1\).\(C_{10}^1\) = 22750
\(\left|B\right|\) = \(C_{15}^2\).\(C_5^2\).\(C_{10}^1\) = 10500
\(\left|C\right|\) = \(C_{15}^2\).\(C_5^1\).\(C_{10}^2\) = 23625
Thay vào (1) ta có \(\left|D\right|\) = 56875
Vậy có 56875 cách chọn đề kiểm tra.
18 tháng 5 2021
Ta dễ có tứ giác ABDE nội tiếp đường tròn đường kính AB => ^CDE = ^BAE
Lại có ^BAE = ^CAD (= 900 - ^ACB), suy ra ^CDE = ^CAD = 900 - ^ACD => DE vuông góc AC
Thấy D,E,P cùng có tung độ bằng 1 => D,E,P thẳng hàng, vì P thuộc AC nên DE vuông góc với AC tại P
Đường thẳng AC: đi qua P(2;1), VTPT \(\overrightarrow{DE}=\left(5;0\right)\) \(\Rightarrow AC:x-2=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\x+y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\Rightarrow A\left(2;0\right)\)
Đường thẳng BC: đi qua \(D\left(-2;1\right)\),VTPT \(\overrightarrow{DA}=\left(4;-1\right)\Rightarrow BC:4x-y+9=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\4x-y+9=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=17\end{cases}\Rightarrow C\left(2;17\right)}\)
Đường thẳng BE: đi qua \(E\left(3;1\right)\), VTPT \(\overrightarrow{AE}=\left(1;1\right)\Rightarrow BE:x+y-4=0\)
Xét hệ: \(\hept{\begin{cases}4x-y+9=0\\x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\Rightarrow B\left(-1;5\right)\)
Vậy \(A\left(2;0\right),B\left(-1;5\right),C\left(2;17\right)\).
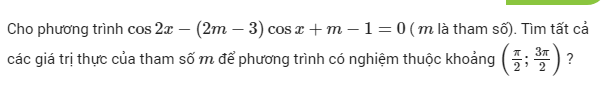
ĐẶT CÂU HỎI CHO TỪ GẠCH CHÂN
My brother wants a glass of lemon juice
-> What does your brother want?
~Study well~
#SJ
ĐẶT CÂU HỎI CHO TỪ GẠCH CHÂN
My brother wants a glass of lemon juice
=> what does your brother want ?
#hok tốt#