K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
19 tháng 2 2022
\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)
7 tháng 3 2022
\(\left(2x-3,5\right)^2+\left(x^2-\dfrac{49}{16}\right)^2=0\)
Vì \(\left(2x-3,5\right)^2\ge0;\left(x^2-\dfrac{49}{16}\right)^2\ge0\)
\(\Rightarrow\left(2x-3,5\right)^2+\left(x^2-\dfrac{49}{16}\right)^2\ge0\)
Mà \(\left(2x-3,5\right)^2+\left(x^2-\dfrac{49}{16}\right)^2=0\)
\(\Rightarrow\left\{{}\begin{matrix}2x-3,5=0\\x^2-\dfrac{49}{16}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{7}{4}\\x=\pm\dfrac{7}{4}\end{matrix}\right.\Rightarrow x=\dfrac{7}{4}\)
23 tháng 2 2022
Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm
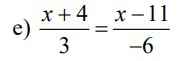
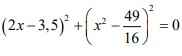
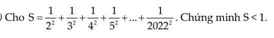
A
A