Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 5:
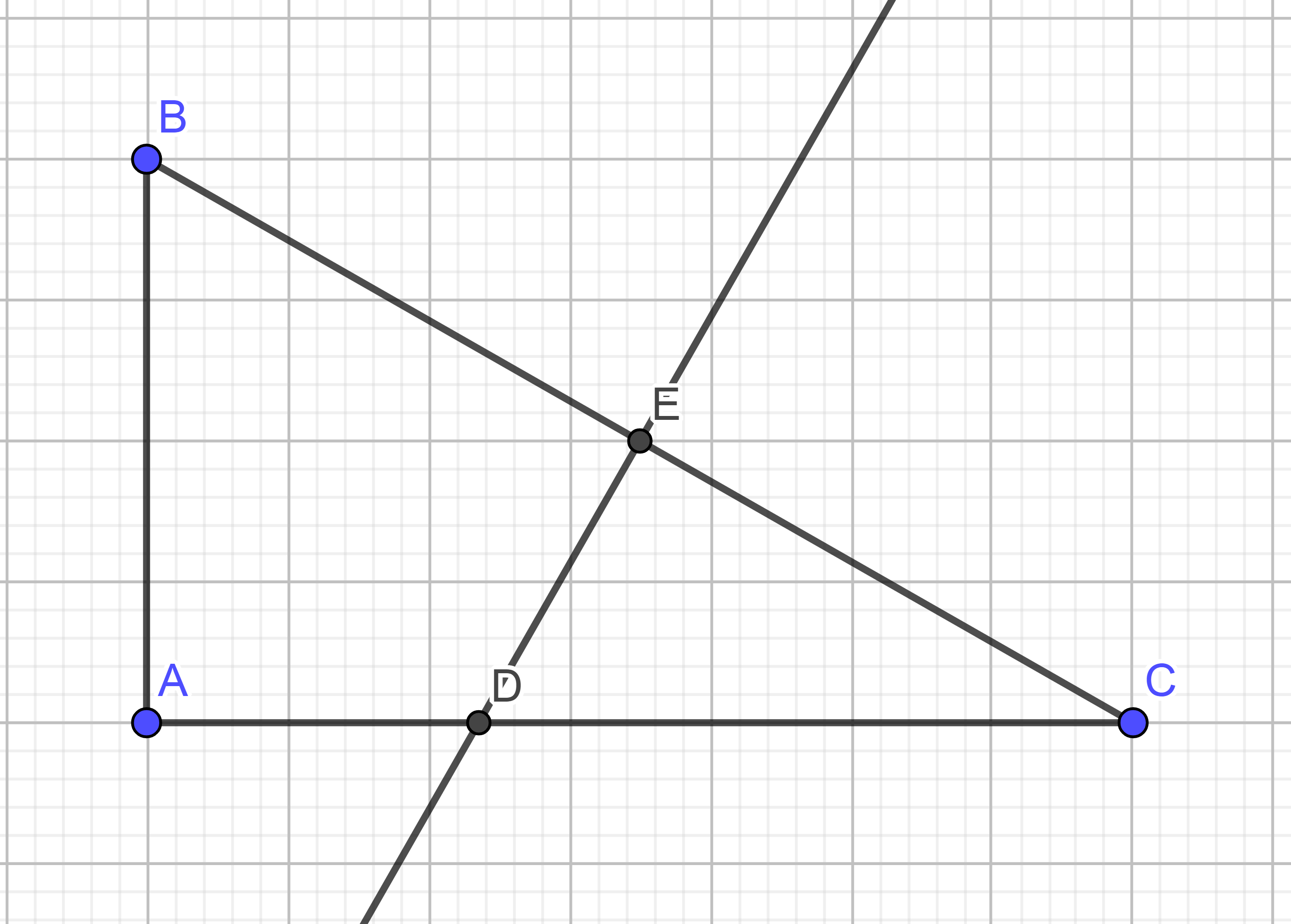
Xét ΔABC vuông tại A
Áp dụng Pytago ta có:
BC2 = AB2 + AC2
= 242 + 322
⇒ BC = 40
DE là trung trực của BC
⇒ E là trung điểm của BC; DE vuông góc với BC tại E
⇒ EC = BC/2 = 40/2 = 20
Xét ΔCED và ΔCAB có:
∠CED = ∠CAB = 90o
∠C chung
⇒ ΔCED đồng dạng ΔCAB
⇒ CE/CA = ED/AB
⇒ 12/32 = ED/24
⇒ ED = 9

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

Bài 2:
Ta có: \(\dfrac{BD}{DC}=\dfrac{3}{7}\)
nên \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
hay \(AB=\dfrac{3}{7}AC\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{49}+AC^2=20^2=400\)
\(\Leftrightarrow AC^2=\dfrac{9800}{29}\)
\(\Leftrightarrow AC=\dfrac{70\sqrt{58}}{29}\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{7}\cdot AC=\dfrac{30\sqrt{58}}{29}\left(cm\right)\)