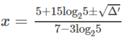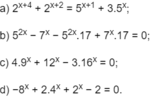Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt t = 3 x (t > 0) , ta có bất phương trình
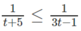
Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.
Từ đó ta có hệ:
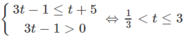
Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

S = 1/4 + 1/42 + 1/43 + ... + 1/450
4S = 4(1/4 + 1/42 + 1/43 + ... + 1/450)
4S = 1 + 1/4 + 1/42 + ... + 1/449
4S - S = (1 + 1/4 + 1/42 + ... + 149) - (1/4 + 1/42 + 1/43 + ... + 1/450)
3S = 1 - 1/450
S = \(\frac{1-\frac{1}{4^{50}}}{3}\)

a) 16. 2 x + 4. 2 x = 5. 5 x + 3. 5 x
⇔ 20. 2 x = 8. 5 x ⇔ (2/5)x = ( 2 / 5 ) 1 ⇔ x = 1
b) 16. 7 x − 16. 5 2 x = 0
⇔ 7 x = 5 2 x ⇔ ( 7 / 25 ) x = ( 7 / 25 ) 0 ⇔ x = 0
c) Chia hai vế cho 12 x ( 12 x > 0), ta được:
4 ( 3 / 4 ) x + 1 − 3 ( 4 / 3 ) x = 0
Đặt t = ( 3 / 4 ) x (t > 0), ta có phương trình:
4t + 1 − 3/t = 0 ⇔ 4 t 2 + t − 3 = 0
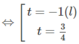
Do đó, ( 3 / 4 ) x = ( 3 / 4 ) 1 . Vậy x = 1.
d) Đặt t = 2 x (t > 0), ta có phương trình:
− t 3 + 2 t 2 + t – 2 = 0
⇔ (t − 1)(t + 1)(2 − t) = 0
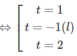
Do đó: 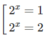

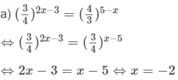
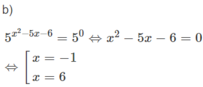
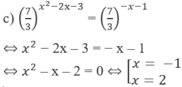
d) Hướng dẫn: Lấy logarit cơ số 2 cả hai vế
Phương trình đã cho có hai nghiệm phân biệt đều thỏa mãn điều kiện