Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi hai góc kề bù lần lượt là a và b
Ta có: a+b=180độ
=>1/2a+1/2b = 1/2(a+b) = 90độ
vẽ hình ra là thấy!!!
Gọi xOy và yOz là 2 góc kề bù, Ot là p/g xOy; Ot' là p/g yOz
Ta có: yOt = 1/2 xOy (vì Ot là tia p/g xOy) (1)
yOt' = 1/2 yOz (vì Ot' là tia p/g yOz) (2)
xOy + yOz = 180 độ ( vì 2 góc kề bù)
Từ (1) và (2) suy ra yOt + yOt' = 1/2(xOy + yOz)
= 1/2.180
= 90 độ
suy ra tOt' = 90 độ
Vậy 2 tia p/g của 2 góc kề bù vuông góc với nhau
Nhớ nha !!!!

a) Vì \(\widehat{xOz}-\widehat{yOz}=4\widehat{yOz}\) nên \(\widehat{xOz}=5\widehat{yOz}\)
Mà \(\widehat{xOz},\widehat{yOz}\) kề bù
\(\Rightarrow\widehat{xOz}+\widehat{yOz}=180^o\)
\(\Rightarrow\widehat{xOz}=180^o:\left(5+1\right).5=150^o\)
\(\Rightarrow\widehat{yOz}=180^o-150^o=30^o\)
Vậy \(\widehat{yOz}=30^o,\widehat{xOz}=150^o\).
b) Trên cùng 1 nửa mặt phẳng có bờ chứa tia Ox, vẽ tia Om sao cho \(\widehat{xOm}=75^o\)
\(\Rightarrow\widehat{xOz}>\widehat{xOm}\left(150^o>30^o\right)\) nên tia Om nằm giữa 2 tia Ox, Oz (1)
Ta có: \(\widehat{xOm}+\widehat{mOz}=\widehat{xOz}\)
\(75^o+\widehat{zOm}=150^o\)
\(\Rightarrow\widehat{zOm}=150^o-75^o=75^o\)
\(\Rightarrow\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}\) (2)
Từ (1), (2) suy ra Om là tia phân giác của góc xOz.
Vậy Om là tia phân giác của góc xOz.
c) Vì On là tia phân giác của góc yOz
\(\Rightarrow\)Tia On nằm giữa 2 tia Oy, Oz và \(\widehat{yOn}=\widehat{nOz}=\frac{\widehat{yOz}}{2}=30^o:2=15^o\)
Mà Oz nằm giữa 2 tia Om, On nên ta có:
\(\widehat{nOz}+\widehat{zOm}=\widehat{mOn}\)
\(15^o+75^o=\widehat{mOn}\)
\(\widehat{mOn}=90^o\) (đpcm)

a)
Sửa đề: Tính \(\widehat{yOz}\)
Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow50^0+\widehat{yOz}=180^0\)
hay \(\widehat{yOz}=130^0\)
Vậy: \(\widehat{yOz}=130^0\)

Bạn tự vẽ hình ra, máy trục trặc nên mình không vẽ được,
Gọi hai góc kề bù là x , y.
Ta có: \(x+y=90^o+90^o=180\)
\(\Rightarrow\frac{1}{2}.x+\frac{1}{2}.y=\frac{1}{2}\left(x+y\right)\)
Mà \(x+y=180^o\)
Vậy \(\frac{1}{2}\left(x+y\right)=\frac{1}{2}.180^o=90^{o^{\left(đpcm\right)}}\)
Trả lời
Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
~Mik ko biết đúng không?~

Gọi \(\widehat{xOz}\), \(\widehat{zOy}\) là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của \(\widehat{xOz}\) , \(\widehat{zOy}\)
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy, nên:
\(\hept{\begin{cases}\widehat{uOz}=\widehat{xOu}=\frac{\widehat{xOz}}{2}\\\widehat{zOv}=\widehat{yOv}=\frac{\widehat{zOy}}{2}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}2\widehat{uOz}=\widehat{xOz}\\2\widehat{zOv}=\widehat{zOy}\end{cases}}\)
Ta lại có:
\(\widehat{xOz}+\widehat{zOy}=180^0\) ( kề bù )
\(\Rightarrow2\widehat{uOz}+2\widehat{zOv}=180^0\)
\(\Rightarrow2\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\)
\(\Rightarrow\left(\widehat{uOz}+\widehat{zOv}\right)=180^0\div2\)
\(\Rightarrow\left(\widehat{uOz}+\widehat{zOv}\right)=90^0\)
\(\Rightarrow\widehat{uOv}=90^0\) (vì 2 góc uOz, góc zOv kề nhau)
\(\Rightarrow\) Tia Ou vuông góc tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
ta có góc AOE+EOC=180
MÀ BOC=AOB, OED=DOC
vậy BOC+DOE=\(\frac{AOE+EOC}{2}=\frac{180}{2}=90\)

Gọi góc xOz và gó zOy là 2 góc kề bù; tia Ou, Ov lần lượt là tia phân giác của xOz và zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông với nhau, ta sẽ chứng minh tia Ou và tia Ov vuông góc với nhau.
* Vì tia Ou, Ov lần lượt là tia phân giác của xOz và zOy nên:
{ góc uOz = 1/2 xOz
{ góc zOv = 1/2 zOy
\(\Rightarrow\)2 góc uOz = xOy
2 góc zOv = zOy
Ta lại có:
xOz + zOy = 180 độ (vì 2 góc xOz, zOy kề bù)
\(\Rightarrow\)2 góc uOz + 2 góc zOv = 180 độ
\(\Rightarrow\)2 x (góc uOz + góc zOv) = 180 độ
\(\Rightarrow\)góc uOz + góc zOv = 90 độ
\(\Rightarrow\)góc uOv = 90 độ (vì 2 góc uOz và zOv kề nhau)
\(\Rightarrow\)tia Ou vuông góc với tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
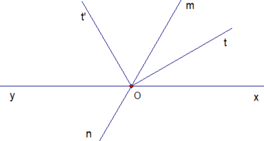

* Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
xet hai goc ke bu xOy va yOz
tia phan giac goc xOy la On ; tia phan giac goc yOz la Om
theo de bai ta co goc nOy = 1/2 xOy
mOy = 1/2 yOz
suy ra mOn = nOy + mOy = 1/2 (xOy + yOz )=1/2.180=90(DPCM!)