Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

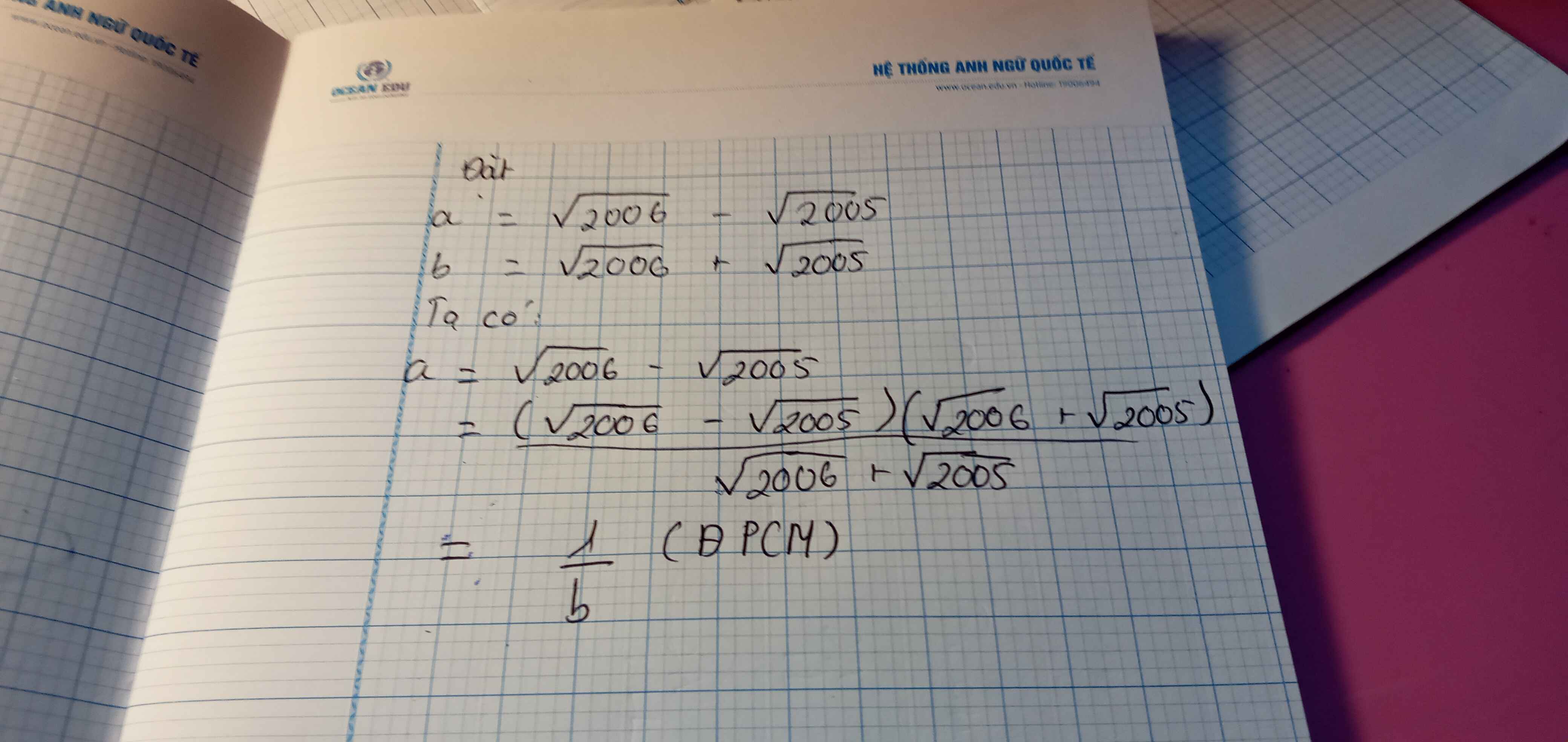
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)

\(\left(x-\sqrt{11}\right)^2=0\)
\(\left(x-\sqrt{11}\right)=0\)
\(x=\sqrt{11}\)
\(\left(x-\sqrt{11}^2=0\right)\)
\(\left(x-\sqrt{11}\right)=0\)
\(x=\sqrt{11}\)

Hai bài này áp dụng hằng đẳng thức \(a^2-b^2=\left(a-b\right)\left(a+b\right)\) bạn nhé
a)
\(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)\)
\(=2^2-\sqrt{3}^2\)
\(=4-3\)
\(=1\)
b)
Hai số nghịch đảo nhau là 2 số có tích của chúng bằng 1
Ví dụ
\(\frac{a}{b}\) và \(\frac{b}{a}\) ( hai số nghịch đảo )
\(\frac{a}{b}.\frac{b}{a}=1\)
Ta có
\(\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)\)
\(=\sqrt{2006}^2-\sqrt{2005}^2\)
\(=2006-2005\)
\(=1\)
=> Đpcm

Đặt \(a=\sqrt{2006}-\sqrt{2005}\) , \(b=\sqrt{2006}+\sqrt{2005}\)
Ta sẽ chứng minh \(a=\frac{1}{b}\)
Ta có : \(a=\sqrt{2006}-\sqrt{2005}=\frac{\left(\sqrt{2006}-\sqrt{2005}\right).\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}\)
\(=\frac{1}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{b}\)
Vậy a và b là hai số nghịch đảo.
Đầu tiên nhắc lại định nghĩ hai số nghịch đảo: Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.
Vd: $ab=1\implies $ a và b là hai số nghịch đảo của nhau và ngược lại nếu a và b là hai số nghịch đảo của nhau thì $ab=1$.
Áp dụng vào bài toán trên ta có: $(\sqrt{2006}-\sqrt{2005})(\sqrt{2006}-\sqrt{2005})=1\implies $ hai số trên là nghịch đảo của nhau.

Nếu tích của 2 số khác nhau bằng 1 thì 2 số đó là số nghịch đảo của nhau
Ta có
\(\left(\sqrt{2006}-\sqrt{2005}\right).\left(\sqrt{2006}+\sqrt{2005}\right)\)
= 2006-2005
=1 ( đpcm)

a) (2-\(\sqrt{3}\))(2+\(\sqrt{3}\))=22-(\(\sqrt{3}\))2=4-3=1 (ĐPCM)
Câu a: Ta có:
(2−√3)(2+√3)=22−(√3)2=4−3=1(2−3)(2+3)=22−(3)2=4−3=1
Câu b:
Ta tìm tích của hai số (√2006−√2005)(2006−2005) và (√2006+√2005)(2006+2005)
Ta có:
(√2006+√2005).(√2006−√2005)(2006+2005).(2006−2005)
= (√2006)2−(√2005)2(2006)2−(2005)2
=2006−2005=1=2006−2005=1
Do đó (√2006+√2005).(√2006−√2005)=1(2006+2005).(2006−2005)=1
⇔√2006−√2005=1√2006+√2005⇔2006−2005=12006+2005
Vậy hai số trên là nghịch đảo của nhau.


(Ghi chú: Muốn chứng minh hai số là nghịch đảo của nhau, ta chứng minh tích của hai số bằng 1.)

a) \(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=2^2-\left(\sqrt{3}\right)^2=4-3=1\)
b) Đặt \(x=\sqrt{2006}-\sqrt{2005},y=\sqrt{2006}+\sqrt{2005}\)
Ta có : \(\frac{1}{x}=\frac{1}{\sqrt{2006}-\sqrt{2005}}=\frac{\sqrt{2006}+\sqrt{2005}}{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}\)
\(=\sqrt{2006}+\sqrt{2005}=y\)
Vì \(y=\frac{1}{x}\) nên hai số này là nghịch đảo của nhau
a) xét \(VT=\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4-\sqrt{3}^2=4-3=1\)
mà \(VT=1\)
\(\Rightarrow VT=VP\left(đpcm\right)\)
b) (lí thuyết) :nếu 2 số nghịch đảo với nhau thì có tích bằng 1 và ngược lại,nếu 2 số có tích bằng 1 thì 2 số đó là nghịch đảo của nhau
Xét \(\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)=2006-2005=1\)
\(\Rightarrow\left(\sqrt{2006}-\sqrt{2005}\right)và\left(\sqrt{2006}+\sqrt{2005}\right)\)là 2 số nghịch đảo với nhau(đpcm)
NHỚ TICK CHO MÌNH NHA !!
MÌNH TRẢ LỜI ĐẦU TIÊN ĐẤY