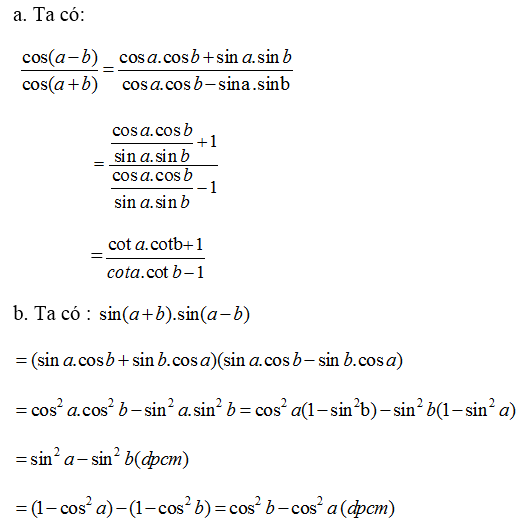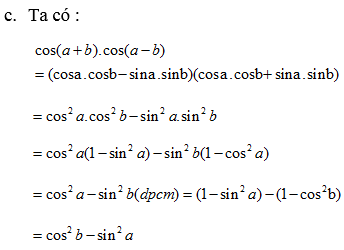Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ \(\frac{A}{2}+\left(\frac{B}{2}+\frac{C}{2}\right)=90^0\)
\(\Rightarrow sin\frac{A}{2}=cos\left(\frac{B}{2}+\frac{C}{2}\right)=cos\frac{B}{2}cos\frac{C}{2}-sin\frac{B}{2}.sin\frac{C}{2}\)
b/ \(\frac{tan^2A-tan^2B}{1-tan^2A.tan^2B}=\frac{\left(tanA-tanB\right)}{\left(1+tanA.tanB\right)}.\frac{\left(tanA+tanB\right)}{\left(1-tanA.tanB\right)}=tan\left(A-B\right).tan\left(A+B\right)\)
\(=tan\left(A-B\right).tan\left(180^0-C\right)=-tan\left(A-B\right).tanC\)
c/
\(A+B+C=180^0\Rightarrow cot\left(A+B\right)=-cotC\)
\(\Leftrightarrow\frac{cotA.cotB-1}{cotA+cotB}=-cotC\)
\(\Leftrightarrow cotA.cotB-1=-cotA.cotC-cotB.cotC\)
\(\Leftrightarrow cotA.cotB+cotB.cotC+cotA.cotC=1\)

phần chứng minh biểu thức không phụ thuộc \(x\)
ta có : \(A=\dfrac{cot^2a-cos^2a}{cot^2a}+\dfrac{sinacosa}{cota}=\dfrac{cot^2a-cos^2a}{cot^2a}+\dfrac{cos^2a}{cot^2a}\)
\(=\dfrac{cot^2a-cos^2a+cos^2a}{cot^2a}=\dfrac{cot^2a}{cot^2a}=1\left(đpcm\right)\)
ý còn lại : xem lại đề nha bn
phần chứng minh đẳng thức
ta có : \(\dfrac{sin2a-2sina}{sin2a+2sina}+tan^2\dfrac{a}{2}=\dfrac{2sinacosa-2sina}{2sinacosa+2sina}+tan^2\dfrac{a}{2}\)
\(=\dfrac{2sina\left(cosa-1\right)}{2sina\left(cosa+1\right)}+tan^2\dfrac{a}{2}=\dfrac{cosa-1}{cosa+1}+tan^2\dfrac{a}{2}\)
\(=\dfrac{1-2sin^2\dfrac{a}{2}-1}{2cos^2\dfrac{a}{2}-1+1}+tan^2\dfrac{a}{2}=\dfrac{-2sin^2\dfrac{a}{2}}{2cos^2\dfrac{a}{2}}+tan^2\dfrac{a}{2}\)
\(=-tan^2\dfrac{a}{2}+tan^2\dfrac{a}{2}=0\left(đpcm\right)\)
ta có : \(\dfrac{sina}{1+cosa}+\dfrac{1+cosa}{sina}=\dfrac{sin^2a+\left(1+cosa\right)^2}{sina\left(1+cosa\right)}\)
\(=\dfrac{sin^2a+cos^2a+2cosa+1}{sina\left(1+cosa\right)}=\dfrac{2cosa+2}{sina\left(cosa+1\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(cosa+1\right)}=\dfrac{2}{sina}\left(đpcm\right)\)
còn 2 câu kia để chừng nào rảnh mk giải cho nha
mk lm 2 câu còn lại nha
ta có : \(\dfrac{sin^2x}{sinx-cosx}-\dfrac{sinx+cosx}{tan^2x-1}=\dfrac{\left(1-cos^2x\right)\left(tan^2x-1\right)-\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}\)
\(=\dfrac{tan^2x-sin^2x-sin^2x-sin^2x+cos^2x}{\left(sinx-cosx\right)\left(tan^2x-1\right)}=\dfrac{\dfrac{sin^4x}{cos^2x}-sin^2x-sin^2x+cos^2x}{\left(sinx-cosx\right)\left(tan^2-1\right)}\)
\(=\dfrac{tan^2x\left(sin^2x-cos^2x\right)-\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}=\dfrac{\left(tan^2x-1\right)\left(sin^2x-cos^2x\right)}{\left(sinx-cosx\right)\left(tan^2x-1\right)}\)
\(=sinx+cosx\left(đpcm\right)\)
ta có : \(\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{1-tan^2a.cot^2b}=\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{1-\dfrac{sin^2a.cos^2b}{cos^2a.sin^2b}}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{\dfrac{cos^2a.sin^2b-sin^2a.cos^2b}{cos^2a.sin^2b}}=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-\left(sin^2a.cos^2b-cos^2a.sin^2b\right)}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-\left(\left(sina.cosb-cosa.sinb\right)\left(sina.cosb+cosa.sinb\right)\right)}\)
\(=\dfrac{sin\left(a+b\right)sin\left(a-b\right).cos^2a.sin^2b}{-sin\left(a-b\right)sin\left(a+b\right)}=-cos^2a.sin^2b\left(đpcm\right)\)
mk lm hơi tắc ! do tối rồi , mà mk lại đang ở quán nek nên không tiện làm dài . bạn thông cảm

\(\frac{cos\left(a-b\right)}{sin\left(a+b\right)}=\frac{cosa.cosb+sina.sinb}{sina.cosb+cosa.sinb}=\frac{\frac{cosa.cosb}{sina.sinb}+1}{\frac{sina.cosb}{sina.sinb}+\frac{cosa.sinb}{sina.sinb}}=\frac{cota.cotb+1}{cota+cotb}\)
Bạn ghi đề ko đúng
\(sin\left(a+b\right)sin\left(a-b\right)=\frac{1}{2}\left[cos2b-cos2a\right]\)
\(=\frac{1}{2}\left[1-2sin^2b-1+2sin^2a\right]\)
\(=sin^2a-sin^2b\)
\(=1-cos^2a-1+cos^2b=cos^2b-cos^2a\)
Câu này bạn cũng ghi đề ko đúng
\(cos\left(a+b\right)cos\left(a-b\right)=\frac{1}{2}\left[cos2a+cos2b\right]\)
\(=\frac{1}{2}\left[2cos^2a-1+1-2sin^2b\right]=cos^2a-sin^2b\)
\(=1-sin^2a-1+cos^2b=cos^2b-sin^2a\)