Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link này nhé.
Câu hỏi của Tan Dang - Toán lớp 7 - Học toán với OnlineMath
a, Trong tam giác ABC có : góc ABC + góc ACB + góc BAC = 180 độ
=> góc ABC + góc ACB =180 độ - góc BAC = 180 độ - 60 độ = 120 độ
Mà BD và CE lần lượt là phân giác của góc ABC ; ACB nên
120 độ = 2.góc IBC + 2.góc ICB = 2.(góc IBC + góc ICB)
=> góc IBC + góc ICB = 120 độ : 2 = 60 độ
Trong tam giác IBC có : góc IBC + góc ICB + góc BIC = 180 độ
=> góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

Gọi IK là đường phân giác của \(BIC\)^
Ta có:B^+C^=180-A^=120
\(\Rightarrow DBC\)^+ECB^=120:2=60
\(\Rightarrow\)BIC^=180-60=120
\(\Rightarrow\)BIE^=180-BIC^=180-120=60(kề bù)
Mà BIC^=120\(\Rightarrow\)BIK^=60
Xét t/g BIK và t/g BIE có:
BIE^=BIK^,IBK^=IBE^,BI chung
\(\Rightarrow\)t/g BIK=t/g BIE(g.c.g)
\(\Rightarrow IE=IK\)
Chứng minh tương tự \(\Rightarrow ID=IK\)
\(\Rightarrow ID=IE\)
Tự vẽ hình
Gọi IK là đường phân giác của góc BIC. Lại có: B^+C^=180∘−A^=180∘−60∘=120∘ ⇒2B1^+2C1^=120∘⇒B1^+C1^=60∘⇒BIC^=180∘−60∘=120∘ Khi đó I1^=I2^=I3^=I4^=60∘ Ta có: B1^=B2^;I1^=I2^;BI: cạnh chung ⇒ΔBIE=ΔBIK(g.c.g)⇒IK=IE Chứng minh tương tự: ID=IK Do đó ID=IE
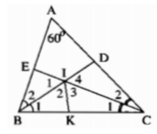
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
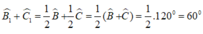
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID

a, Trong tam giác ABC có : góc ABC + góc ACB + góc BAC = 180 độ
=> góc ABC + góc ACB =180 độ - góc BAC = 180 độ - 60 độ = 120 độ
Mà BD và CE lần lượt là phân giác của góc ABC ; ACB nên
120 độ = 2.góc IBC + 2.góc ICB = 2.(góc IBC + góc ICB)
=> góc IBC + góc ICB = 120 độ : 2 = 60 độ
Trong tam giác IBC có : góc IBC + góc ICB + góc BIC = 180 độ
=> góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ