Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Đồ thị hàm số:
2.
Phương trình hoành độ giao điểm:
\(\dfrac{x^2}{4}=\dfrac{-x}{2}+2\)
\(\Leftrightarrow\dfrac{x^2}{4}+\dfrac{x}{2}-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
\(x=2\Rightarrow y=1\Rightarrow\left(2;1\right)\)
\(x=-4\Rightarrow y=4\Rightarrow\left(-4;4\right)\)
3.
Phương trình tiếp tuyến của \(\left(P\right)\) có dạng \(y=ax+b\left(d'\right)\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow-\dfrac{1}{2}=a;b\ne2\Rightarrow y=-\dfrac{1}{2}x+b\left(d'\right)\)
Phương trình hoành độ giao điểm của \(\left(d\right);\left(P\right)\)
\(-\dfrac{1}{2}x+b=\dfrac{x^2}{4}\Leftrightarrow\dfrac{1}{4}x^2+\dfrac{1}{2}x-b=0\left(1\right)\)
\(\Delta'=\dfrac{1}{4}+b=0\Leftrightarrow b=-\dfrac{1}{4}\)
\(\Rightarrow y=-\dfrac{1}{2}x-\dfrac{1}{4}\left(d'\right)\)
\(\left(1\right)\Leftrightarrow\dfrac{1}{4}x^2+\dfrac{1}{2}x+\dfrac{1}{4}=0\Leftrightarrow x=-1\Rightarrow y=\dfrac{1}{4}\)
\(\Rightarrow\left(-1;\dfrac{1}{4}\right)\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-\dfrac{1}{4}x^2-\dfrac{1}{2}x=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}x\left(\dfrac{1}{2}x+1\right)=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(0;0\right);\left(-2;-1\right)\right\}\)
c: Gọi M(2y;y)
Thay x=2y và y=y vào (P), ta được:
\(y=\dfrac{-1}{4}\cdot\left(2y\right)^2=\dfrac{-1}{4}\cdot4y^2=-y^2\)
=>y(y+1)=0
=>y=0 hoặc y=-1
=>x=0 hoặc x=-2

a. Em tự giải
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
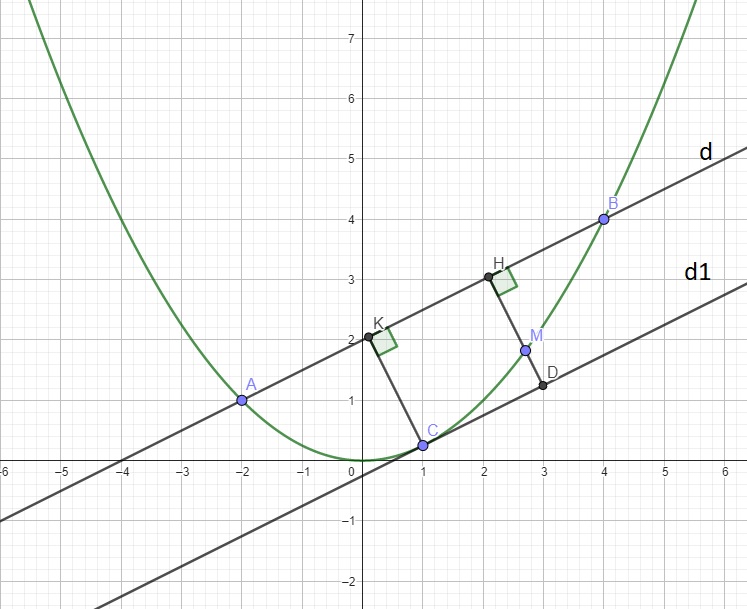
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)

b: Vì (d) cắt y=-x+2 tại trục tung nên
a<>-1 và b=2
=>y=ax+2
Thay x=1 và y=3 vào y=ax+2, ta được:
a+2=3
=>a=1
c: Thay x=3y vào y=-x+2, ta được;
y=-3y+2
=>4y=2
=>y=1/2
=>B(3/2;1/2)

a, - Thay tọa độ hai điểm xA, xB vào (P) ta được : \(\left\{{}\begin{matrix}y_A=2\\y_B=\dfrac{1}{2}\end{matrix}\right.\)
=> Tọa độ 2 điểm A, B lần lượt là : \(\left(2;2\right),\left(-1;\dfrac{1}{2}\right)\) .
b, - Gọi phương trình đường thẳng AB có dạng : y = ax + b .
- Thay tọa độ A, B vào phương trình ta được hệ : \(\left\{{}\begin{matrix}2a+b=2\\-a+b=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)
- Thay lại a, b vào phương trình ta được : \(y=\dfrac{1}{2}x+1\)
Vậy ...