Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
\(C=2r\cdot3.14=r\cdot6.28\)
Vậy: C và r là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ k=6,28
Câu 2:
Vì x và y là hai đại lượng tỉ lệ thuận
nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
a: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
nên \(\dfrac{x_1}{-2}=\dfrac{4}{6}=\dfrac{2}{3}\)
hay \(x_1=\dfrac{-4}{3}\)
b: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
\(\Leftrightarrow\dfrac{x_1}{-3}=\dfrac{y_1}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{-3}=\dfrac{y_1}{4}=\dfrac{y_1-x_1}{4-\left(-3\right)}=\dfrac{-2}{7}\)
Do đó: \(x_1=\dfrac{6}{7};y_1=-\dfrac{8}{7}\)

Lời giải:
Vì $x,y$ tỉ lệ nghịch nên tích $xy$ không đổi
a.
Ta có:
$x_2y_2=x_1y_1=-45$
$\Rightarrow y_2=\frac{-45}{x_2}=\frac{-45}{9}=-5$
b.
$x_1y_1=x_2y_2$
$2y_1=4y_2$
$y_1=2y_2$. Thay vô $y_1+y_2=-12$ thì:
$2y_2+y_2=-12$
$3y_2=-12$
$y_2=-4$
$y_1=2y_2=2(-4)=-8$
c.
$x_1y_1=x_2y_2$
$12x_1=3y_2$
$4x_1=y_2$
Thay vô $x_1+2y_2=18$ thì:
$x_1+2.4x_1=18$
$9x_1=18$
$x_1=2$
$y_2=4x_1=4.2=8$

Bài 2:
a: Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
=>x=5k; y=3k
xy=1500
nên \(k^2=100\)
Trường hợp 1: k=10
=>x=50; y=30
Trường hợp 2: k=-10
=>x=-50; y=-30

\(\text{Gọi hstl là }a\\ \Rightarrow x_1y_1=x_2y_2=a\\ \Rightarrow\dfrac{y_1}{x_2}=\dfrac{y_2}{x_1}=\dfrac{y_1}{5}=\dfrac{y_2}{6}=\dfrac{8y_1-5y_2}{40-30}=\dfrac{50}{10}=5\\ \Rightarrow\left\{{}\begin{matrix}y_1=25\\y_2=30\end{matrix}\right.\\ \Rightarrow a=x_1y_1=25\cdot6=150\)

Ta có: x và y là hai đại lượng tỉ lệ nghịch nên ta có:
xy = x1.y1 = x2.y2
hay 3y1 = 2y2
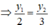
Theo đầu bài: y1 + y2 = 13
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
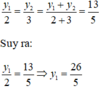
Do đó x1.y1 = 3.(26/5) = 78/5
Vậy xy = 78/5, hay y = 78/5x