

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Có hình vẽ :
Dễ thấy SABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)
mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)
=> SABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)
Khi 2 đường chéo vuông góc với nhau thì
\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)
hay \(sin\alpha=1\)
Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm)

Làm như sau :
Kẻ AH vg BD ; CK vg BD
Sabd = 1/2.AH.BD (1)
Sbcd = 1/2.CK.BD (2)
từ (1) và (2) => Sabcd= Sabd + Sbcd = 1/2BD ( AH+CK) (*)
Tam giác AHO vuông tại H , theo tỉ số lượng giác giữa cạnh và góc
=> AH = OA . sin AOH (3)
Tương tự CK = OC.sin BOC (4)
Mà BOC = AOH => sin BOC = sin AOH (5)
Từ (3) và (4) và (5) => AH + CK = sin AOH ( OA + OC ) = AC .sin AOH (**)
Từ (*) và (**) => cái cần phải CM

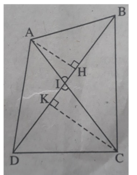
Giả sử hai đường chéo AC, BD cắt nhau tại I, ∠ (AIB) = α là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sin α , CK = CI.sin α
Diện tích tam giác ABD là S A B D = 1/2 BD.AH.
Diện tích tam giác CBD là S C B D = 1/2 BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = S A B D + S C B D = 1/2BD.(AH + CK)
= 1/2 BD.(AI + CI)sin α = 1/2BD.AC.sin α

\(\left(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\right).\dfrac{1}{\sqrt{1+tan^2\alpha}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1+sin\alpha\right)\left(1-sin\alpha\right)}}\right).\dfrac{1}{\sqrt{1+\left(\dfrac{sin\alpha}{cos\alpha}\right)^2}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{1-sin^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{1-sin^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{1}{cos^2\alpha}}}\)
\(=\left(\dfrac{1+sin\alpha}{cos\alpha}+\dfrac{1-sin\alpha}{cos\alpha}\right).\dfrac{1}{\dfrac{1}{cos\alpha}}=\dfrac{2}{cos\alpha}.cos\alpha=2\)