Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

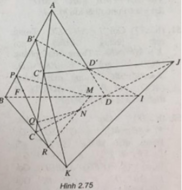
a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C'B'D')
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt

Chọn đáp án B
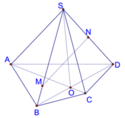
+ Giả sử SO, AD cắt nhau. Khi đó SO, AD đồng phẳng, suy ra S thuộc mp (ABCD) (Vô lý). Đáp án A bị loại.
+ Giả sử MN cắt SC. Khi đó MN và SC đồng phẳng, suy ra C thuộc (SBD) (Vô lý). Do đó đáp án C bị loại.
+ Giả sử SA cắt BC. Khi đó SA, BC đồng phẳng. Suy ra S thuộc mp (ABCD) (Vô lý). Đáp án D bị loại. MN, SO cùng nằm trong mp (SBD), không song song và trùng nhau.

Dễ thấy P là điểm chính giữa nên D,N,P thẳng hàng
Cần chứng minh
Ta có :
b) Theo câu a suy ra
Mà cân tại I ( do IP = ID ) nên
Suy ra
c) từ câu b ( 1 )
Theo hệ thức lượng, ta có :
Do đó :
Suy ra ( 2 )
Từ ( 1 ) và ( 2 ) kết hợp với IM // PN suy ra A,M,N thẳng hàng

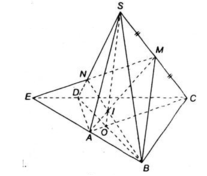
a) + Trong mp(ABCD), AB cắt CD tại E.
E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)
E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)
Mà M ∈ SC ⊂ (SCD)
⇒ ME ⊂ (SCD).
+ Trong mp(SCD), EM cắt SD tại N.
Ta có:
N ∈ SD
N ∈ EM ⊂ mp(MAB)
Vậy N = SD ∩ mp(MAB)
b) Chứng minh SO, MA, BN đồng quy:
+ Trong mặt phẳng (SAC) : SO và AM cắt nhau.
+ trong mp(MAB) : MA và BN cắt nhau
+ trong mp(SBD) : SO và BN cắt nhau.
+ Qua AM và BN xác định được duy nhất (MAB), mà SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.
Vậy SO, MA, BN đồng quy.

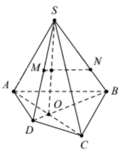

Đặt \(\frac{AB}{CD}=k\)
Do AB // CD nên \(\frac{EA}{EC}=\frac{EB}{ED}=k\) và \(\frac{FA}{FD}=\frac{FB}{FC}=k\) (như hình vẽ)
Suy ra : \(\overrightarrow{EA}=-k\overrightarrow{EC}\), \(\overrightarrow{EB}=-k\overrightarrow{ED}\) , \(\overrightarrow{FA}=-k\overrightarrow{FD}\) và \(\overrightarrow{FB}=-k\overrightarrow{FC}\)
Do M là trung điểm AB và N là trung điểm CD nên :
\(2\overrightarrow{EM}=\overrightarrow{EA}+\overrightarrow{EB}=-k\overrightarrow{EC}-k\overrightarrow{ED}=-2\left(\overrightarrow{EC}+\overrightarrow{ED}\right)=-2k\overrightarrow{EN}\)
Suy ra \(\overrightarrow{EM}=k\overrightarrow{EN}\) (1)
Hoàn toàn tương tự cũng được \(\overrightarrow{FM}=k\overrightarrow{FN}\) (2)
Từ (1) và (2) suy ra điều cần chứng minh