Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
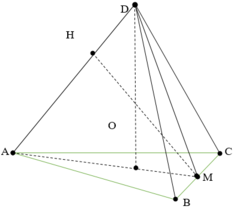
Gọi O là trọng tâm ∆ABC
Kẻ AM ⊥ AC và MH ⊥ AD
Vì DABC là tứ diện đều => DO ⊥ (ABC)
Vì ∆ABC đều => AO = ![]()
Xét ∆DAO vuông tại O

Ta có: DO ⊥ BC và AM ⊥ BC
=> (DAM) ⊥ BC
=> MH ⊥ BC
Lại có MH ⊥ DA
=> MH = d(BC, DA)
Xét ∆DAM, ta có:
DO.AM = MH.AD
⇔ MH = a 2 2
⇔ d(BC, DA) = a 2 2

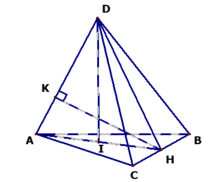
Tính khoảng cách giữa AD và BC.
● Trong ΔADH vẽ đường cao HK tức là HK ⊥ AD (1)
- Mặt khác BC ⊥ (ADH) nên BC ⊥ HK (2)
- Từ (1) và (2) ta suy ra d(AD, BC) = HK.
● Xét ΔDIA vuông tại I ta có:
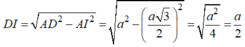
● Xét ΔDAH ta có:
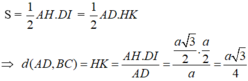

\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)

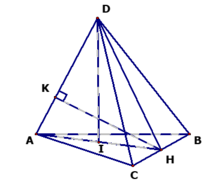
CMR: BC ⊥ (ADH) và DH = a.
● Δ ABC đều, H là trung điểm BC nên AH BC, AD BC
⇒ BC ⊥ (ADH) ⇒ BC ⊥ DH.
⇒ DH = d(D, BC) = a

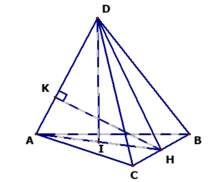
CMR: DI ⊥ (ABC).
● AD = a, DH = a ΔDAH cân tại D.
- Mặt khác I là trung điểm của AH nên DI ⊥ AH.
● BC ⊥ (ADH) ⇒ BC ⊥ DI.
⇒ DI ⊥ (ABC).
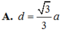
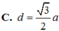

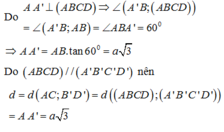
Đáp án B.
Gọi lần lượt là trung điểm của AD và BC. Ta có ∆ ABD và ∆ ACD đều cạnh bằng a nên
=> ∆ MBC cân tại M và MN là đường cao của ∆ MBC => MN ⊥ BC
Tương tự, ∆ NAD cân tại N nên NM là đường cao của ∆ NAD => NM ⊥ AD
Suy ra MN là đoạn vuông góc cung của AD và BC.
Vậy