Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
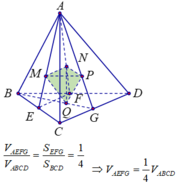
(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
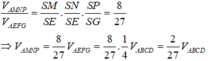
Do mặt phẳng (MNP) (BCD) nên
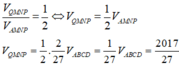

Chọn C

Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác SAB, SAD, SAC.
Gọi I, J lần lượt là trung điểm của AB, AC thì

Qua G₁ dựng đường song song với AB, cắt SA, SB lần lượt tại M, N.
Qua N dựng đường song song với BC, cắt SC tại P.
Qua P dựng đường song song với CD, cắt SD tại Q.
=> Thiết diện của hình chóp S. ABCD khi cắt bới (G₁G₂G₃) là tứ giác MNPQ.


Đáp án D
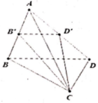
Áp dụng công thức tính tỉ số thể tích, ta có
V A . B ' C D ' V A . B C D = A B ' A B . A C A C . A D ' A D = 1 4
⇔ V A . B ' C D ' = V 4
Mà V A . B C D = V A . B ' C D ' + V C . B D D ' B '
⇒ V C . B D D ' B ' = V - V 4 = 3 V 4

Chọn D
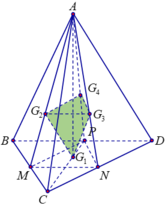
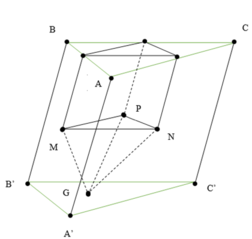
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay 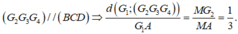
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1
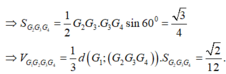
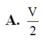
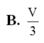
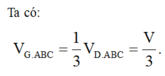
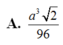
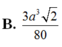
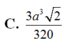
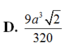

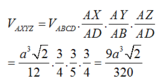
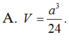
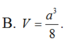
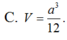
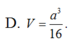
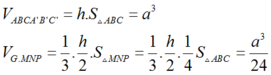
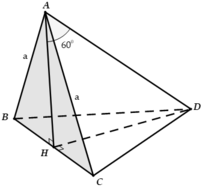

Chọn B
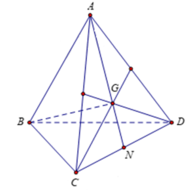
Ta có