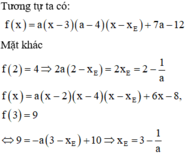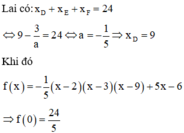Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C/m 3 điểm thẳng hàng là tìm trọng tâm của tam giác đóa pạn, có trọng tâm ròi =>D,M.F thẳng hàng
Hic, vừa đọc xong đề bài đã buồn ngủ rồi!
hình như trên
+)Ta có: ( g-c-g) ( Vì cùng bằng )
Nên MD = NE.
+)Xét và :
( Hai góc đối đỉnh)
Nên ( cgv - gn)
+)Từ B và C kẻ các đường thẳng lần lượt vuông
Góc với AB và AC cắt nhau tại J.
Ta có:
Nên J thuộc AL đường trung trực ứng với BC
Mặt khác : Từ ( Câu a)
Ta có : BM = CN
BJ = CJ ( cm trên)
Nên ( c-g-c)
hay đường trung trực của MN
Luôn đi qua điểm J cố định.
a) Xét \(\Delta AKB\) và \(\Delta AKC\) , có :
AK là cạnh chung
AB = AC ( gt )
BK = KC ( K là trung điểm của BC )
=> \(\Delta AKB=\Delta AKC\left(cgc\right)\)
Ta có :
+ Góc AKB = AKC ( \(\Delta AKB=\Delta AKC\) )
Mà góc AKB + AKC = 1800 ( 2 góc kề bù )
=> AKB = AKC= \(\frac{180^0}{2}\)= 900
Vậy AK \(\perp BC\)
b)
Ta có :
AK \(\perp BC\) ( Theo câu a )
EC \(\perp BC\) ( gt )
=> EC // AK
c) Tam giác BCE là tam giác vuông
GÓC BEC = 500
