Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác AHI và tam giác AKI có:
góc AHI= góc AKI(= 90 độ)
AI chung
góc HAI= góc KAI( phân giác góc A)
=>tam giác AHI= tam giác AKI( g.c.g)
=> HI= IK( cạnh tương ứng)
Xét tam giác BHI và CKI có:
góc BHI= CKI(= 90 độ)
HI= IK( chứng minh trên)
IB= IC( vì là đường trung trực)
=> tam giác BHI= tam giác CKI( c.g.c)
=> BH= CK( cạnh tương ứng) (đpcm)
a, Xét tam giác AHI và tam giác AKI có:
góc AHI= góc AKI(= 90 độ)
AI chung
góc HAI= góc KAI( phân giác góc A)
=>tam giác AHI= tam giác AKI( g.c.g)
=> HI= IK( cạnh tương ứng)
Xét tam giác BHI và CKI có:
góc BHI= CKI(= 90 độ)
HI= IK( chứng minh trên)
IB= IC( vì là đường trung trực)
=> tam giác BHI= tam giác CKI( c.g.c)
=> BH= CK( cạnh tương ứng) (đpcm)

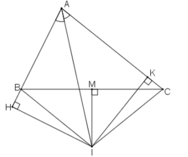
Gọi đường trung trực của BC cắt BC tại M.
Xét ΔBMI và ΔCMI, ta có:
∠(BMI) = ∠(CMI) = 90o (gt)
BM = CM ( vì M là trung điểm của BC )
MI cạnh chung
Suy ra: ΔBMI = ΔCMI(c.g.c)
Suy ra: IB = IC ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIHA và ΔIKA, ta có:
∠(HAI) = ∠(KAI) ( vì AI là tia phân giác của góc BAC).
∠(IHA) = ∠(IKA) = 90o
AI cạnh huyền chung
Suy ra: ΔIHA = ΔIKA(cạnh huyền góc nhọn)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông ΔIHB và ΔIKC, ta có:
IB = IC ( chứng minh trên )
∠(IHB) =∠(IKC) =90o
IH = IK (chứng minh trên)
Suy ra: ΔIHB = ΔIKC(cạnh huyền.cạnh góc vuông)
Suy ra: BH = CK(hai cạnh tương ứng)
