Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
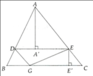
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật


a, xét tam giác ABC và tam giác DAB có:
góc BAC = góc ADB=90 độ
góc ABC = góc BAD( so le trong của Ax//BC)
do đó: tam giác ABC đồng dạng với tam giác DAB(g-g)
b, áp dụng định lí pytago vào tam giác ABC vuông tại A có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\)
theo cm câu a : tam giác ABC đồng dạng với tam giác DAB
=>\(\frac{AB}{AD}=\frac{BC}{AB}=\frac{AC}{BD}\)
\(\Rightarrow AD=\frac{AB^2}{BC}=\frac{15^2}{25}=9cm\)
\(BD=\frac{AB.AC}{BC}=\frac{15.20}{25}=12cm\)
c, \(S_{ABD}=\frac{1}{2}.AD.BD=\frac{1}{2}.9.12=54cm^2\)
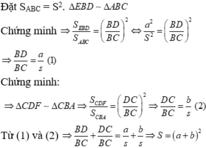
+) AP // BC => S ( BCP ) = S ( BAC ) = S (1)
+) AP //BC => Theo talet: \(\frac{PN}{NM}=\frac{AN}{NC}=\frac{1}{2}\)( vì AC = 3AN )
Theo menelaus xét trong tam giác PMC
\(\frac{CQ}{PQ}.\frac{NP}{NM}.\frac{BM}{BC}=1\)=> \(\frac{CQ}{PQ}.\frac{1}{2}.\frac{1}{3}=1\)=> CQ = 6PQ => CP = 7 QP
=> \(\frac{S\left(QPB\right)}{S\left(CPB\right)}=\frac{QP}{CP}=\frac{1}{7}\)
=> S ( QPB ) = S/7
Có AB//PM => \(\frac{PI}{IB}=\frac{IN}{IA}\left(1\right)\)
Có AD//BC \(\Rightarrow\frac{DI}{IB}=\frac{IA}{IC}\left(2\right)\)
Từ (1)(2) => \(\frac{IN}{IA}=\frac{IA}{IC}\Rightarrow IA^2=IN\cdot IC\)
Xét \(\Delta PMC\) cắt tuyến BQ. Áp dụng Menelaus
\(\Rightarrow\frac{PQ}{QC}\cdot\frac{CB}{BM}\cdot\frac{MN}{NP}=1\)
\(\Leftrightarrow\frac{PQ}{QC}\cdot\frac{3}{1}\cdot\frac{2}{1}=1\Rightarrow\frac{PQ}{QC}=\frac{1}{6}\Rightarrow\frac{PQ}{PC}=\frac{1}{7}\)
Có \(S_{ABC}=S_{PBC}\Rightarrow S_{PBQ}=\frac{1}{7}S=\frac{S}{7}\)