Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK

a: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CA=CB
CI chung
Do đó: ΔCIA=ΔCIB
Suy ra: IA=IB
b: Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó: ΔCHI=ΔCKI
Suy ra: IH=IK
c: IA=IB=AB/2=6(cm)
nen IC=8(cm)
d: Xét ΔCAB có CH/CA=CK/CB
nên HK//AB

BẠn tự vẽ hình nha:
MÌnh không chắc cách làm này phù hợp không,đây là cách chậm và dễ hiểu nhất:
a)Vì ACI+AIC+CAI=1800( tổng 3 góc cua 1 tam giác)
=> ACI+CAI=900 (1)
Vì CIB+IBC+BCI=180(như trên)
=>IBC+BCI=900 (2)
Mà IBC=CAI (tam giac ACB cân- có CA=CB=10 Cm)
=> tu 1 và 2 =>ACI=BCI
Xét tam giác CAI và CBI, có:
ACI=BCI( ở trên)
CAI=CBI (tam giác ABC cân)
CA=CB=10 cm
=> tam giác CAI= tg CBI
=>AI=BI ( 2 cạnh tương ứng)
b) Xét tg CHI và CKI, có:
HCI=KCI (vì có BCI=ACI-câu a)
CI cạnh chung
=> tg CHI= tg CKI ( cạnh huyền-góc nhọn)
=> HI= KI
c) IA=IB(câu a) => IA = AB :2=12:2=6 (cm)
Áp dụng định lí Py-ta-go trong tg CBI,có:
IC2=CB2-IB2
=> IC=8(cm) (bạn tự lắp số vào nha)
d) vì tg CHI=tg CKI (cm ở b)
=> CH=CK => tg CHK cân ở C => CHK=CKH=(1800-HCK):2 (1)
tg CAB cân=> CAB=CBA=(1800-ACB):2=(1800-HCK):2 (2)
từ 1)và (2)=>CHK=CAB
MÀ chúng là 2 góc đồng vị
=>HK song song AB

a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

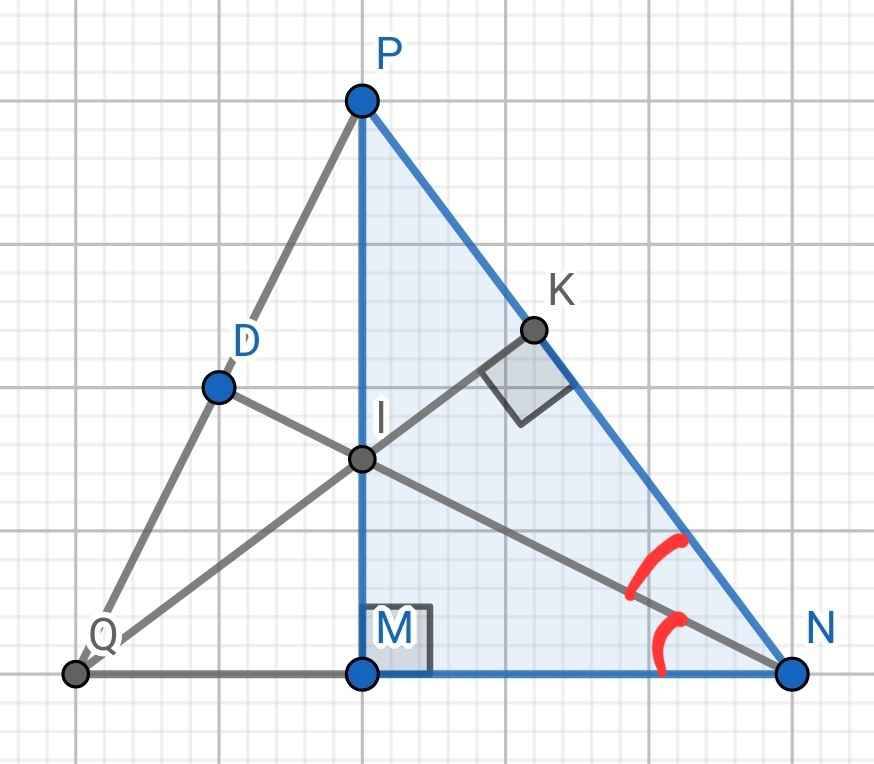
| GT | △MNP cân tại P. MN = 6cm, NPI = MPI = NPM/2 , (I IK ⊥ PM , IH ⊥ PN . IQ = IM |
KL | a, △MPI = △NPI b, HIP = PIK c, △MIQ vuông cân. MQ = ? d, Nếu PKH đều, điều kiện △MNP |
Bài làm:
a, Vì △MNP cân tại P => PN = PM
Xét △NPI và △MPI
Có: NP = MP (gt)
NPI = MPI (gt)
PI là cạnh chung
=> △NPI = △MPI (c.g.c)
b, Xét △HPI vuông tại H và △KPI vuông tại K
Có: PI là cạnh chung
HPI = KPI (gt)
=> △HPI = △KPI (ch-gn)
=> HIP = PIK (2 góc tương ứng)
Mà IP nằm giữa IH, IK
=> IP là phân giác KIH
c, Ta có: PIN = MIQ (2 góc đối đỉnh)
Mà PIN = 90o (gt)
=> MIQ = 90o (1)
Xét △MIQ có: IQ = IM => △MIQ cân tại I (2)
Từ (1), (2) => △MIQ vuông cân tại I
Vì △NPI = △MPI (cmt)
=> IN = IM (2 cạnh tương ứng)
Mà MN = IN + IM = 6 (cm)
=> IN = IM = 6 : 2 = 3 (cm)
Mà IM = IQ
=> IM = IQ = 3 (cm)
Xét △MIQ vuông tại I có: IQ2 + IM2 = MQ2 (định lý Pitago)
=> 32 + 32 = MQ2
=> 9 + 9 = MQ2
=> 18 = MQ2
=> MQ = \(\sqrt{18}=3\sqrt{2}\)
d, Để △PHK đều <=> HPK = PKH = KHP = 60o
=> △MNP có NPM = 60o mà △MNP cân
=> △MNP đều
Vậy để △PKH đều <=> △MNP đều
 MN)
MN)
e) Gọi O là giao điểm của IP và HK. Chứng minh \(\widehat{MON}\) = 180o + \(\widehat{PMO}+\widehat{PNO}+\widehat{HIK}\)